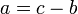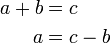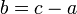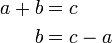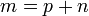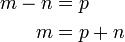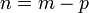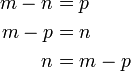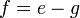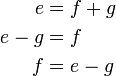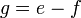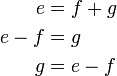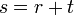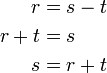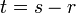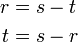Kes-kes berlainan
-
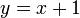
- Bila
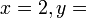
- Bila
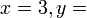
-
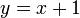
- Bila
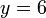 , cari nilai
, cari nilai 
- Bila
-
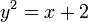
- Bila
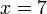 , cari nilai
, cari nilai 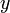
- Bila
-
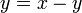
- Bila
 , cari nilai
, cari nilai 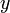
- Bila
Terma
- Pemalar :
- Pembolehubah :
Subjek untuk formula
Untuk formula-formula di bawah
Bukan subjek
Cari nilai
Diberi 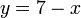
- a) Cari nilai
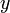 jika
jika 
- b) Cari nilai
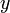 jika
jika 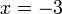
Diberi 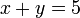
- a) Cari nilai
 jika
jika 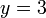
- b) Cari nilai
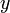 jika
jika 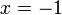
Diberi 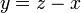
- a) Cari nilai
 jika
jika 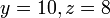
- b) Cari nilai
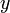 jika
jika 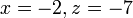
- c) Cari nilai
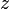 if
if 
Latihan 1
I) Diberi 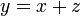
- a) Cari nilai
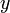 jika
jika 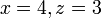
- Jwp :
- b) Cari nilai
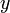 jika
jika 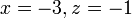
- Jwp :
- c) Cari nilai
 jika
jika 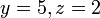
- Jwp :
- d) Cari nilai
 jika
jika 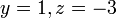
- Jwp :
- e) Cari nilai
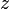 jika
jika 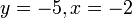
- Jwp :
- f) Cari nilai
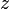 jika
jika 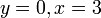
- Jwp :
II) Diberi 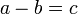
- a) Cari nilai
 jika
jika 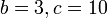
- Jwp :
- b) Cari nilai
 jika
jika 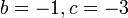
- Jwp :
- c) Cari nilai
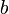 jika
jika 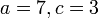
- Jwp :
- d) Cari nilai
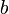 jika
jika 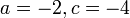
- Jwp :
- e) Cari nilai
 jika
jika 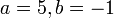
- Jwp :
Jadikan sebagai subjek
Diberi 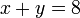
- a) Jadikan
 sebagai subjek / Ungkapkan
sebagai subjek / Ungkapkan  dalam sebutan
dalam sebutan 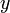
- b) Jadikan
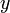 sebagai subjek
sebagai subjek
Bentuk setara / tidak setara
Kadang-kala terdapat lebih daripada satu bentuk jawapan untuk formula, tetapi kedua-dua jawapan adalah setara. Yang manakah di bawah yang sama / tidak sama?
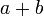 dan
dan 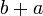
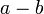 dan
dan 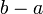
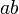 dan
dan 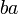
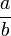 dan
dan 
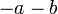 dan
dan 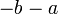
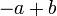 dan
dan 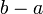
Contoh
Jadikan  sebagai the subjek
sebagai the subjek
- a)
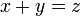
- b)
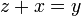
- c)
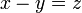
- d)
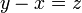
- e)
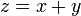
- f)
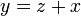
- g)
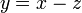
- h)
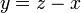
Latihan 2
Jadikan kuantiti di dalam [] sebagai subjek
- a)
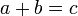
- i)
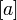
- Jwp :
- Peny :
- i)
- ii)
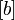
- Jwp :
- Peny :
- b)
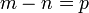
- i)
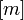
- Jwp :
- Peny :
- i)
- ii)
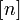
- Jwp :
- Peny :
- c)
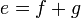
- i)
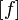
- Jwp :
- Peny :
- i)
- ii)

- Jwp :
- Peny :
- d)
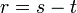
- i)
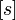
- Jwp :
- Peny :
- i)
- ii)
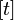
- Jwp :
- Peny :
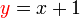
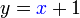 ialah 2
ialah 2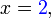
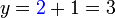
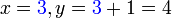
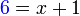
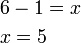
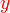 merupakan subjek
merupakan subjek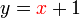
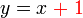 yang "mengacau"
yang "mengacau"  bukan/belum merupakan subjek
bukan/belum merupakan subjek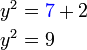
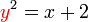 sudah berada di sebelah kanan, kita mendapati bahawa langkah pengiraan tambahan diperlukan kerana ada operasi
sudah berada di sebelah kanan, kita mendapati bahawa langkah pengiraan tambahan diperlukan kerana ada operasi 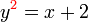 pada-nya. Jadi kita nampak bahawa subjek sepatutnya tiada benda lain yang ditambah/tolak/darab/bahagi-nya dan juga tiada operasi lain ke atasnya.
pada-nya. Jadi kita nampak bahawa subjek sepatutnya tiada benda lain yang ditambah/tolak/darab/bahagi-nya dan juga tiada operasi lain ke atasnya.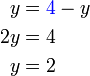
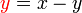 sudah berada di sebelah kanan, dan tiada operasi ke atasnya. Pengiraan tambahan diperlukan kerana
sudah berada di sebelah kanan, dan tiada operasi ke atasnya. Pengiraan tambahan diperlukan kerana 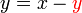 juga berada di sebelah yang satu lagi
juga berada di sebelah yang satu lagi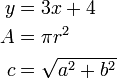
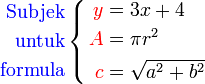
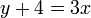
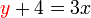 BUKAN subjek
BUKAN subjek
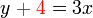
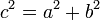
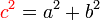 BUKAN subjek
BUKAN subjek
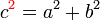
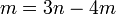
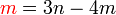 BUKAN subjek
BUKAN subjek
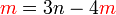
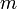 ada juga di sebelah kanan. Subjek hanya boleh wujud satu kali.
ada juga di sebelah kanan. Subjek hanya boleh wujud satu kali.
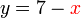 , sekarang kita tahu
, sekarang kita tahu 
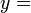
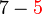
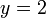
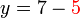
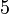 dan oleh itu
dan oleh itu 
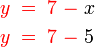
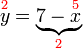 Betul
Betul 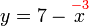
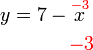
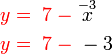
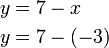
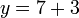
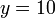
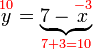
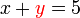
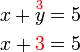
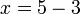
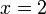
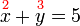 Betul
Betul 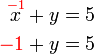

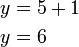
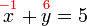

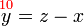
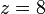
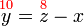
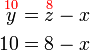
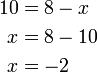 (atau apa-apa cara lain)
(atau apa-apa cara lain)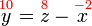
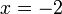
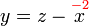
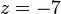
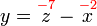
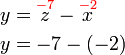
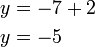
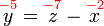
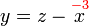
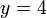
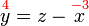
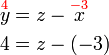
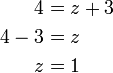
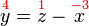
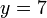
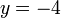
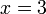
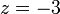
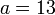
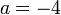
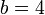
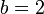
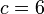

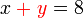
%3d8).png)
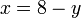
 ?
? 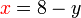

%2by%3d8).png)
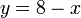

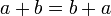
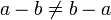
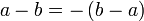
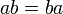
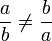
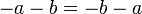
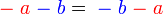
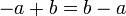
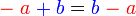
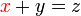
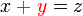
%3dz).png)
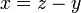

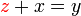
%2bx%3dy).png)
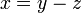
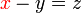
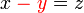
%3dz).png)
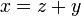
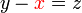
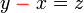
%3dz).png)
%3dovalbox(%2bz)).png)
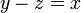


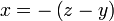
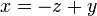 yang juga sama dengan
yang juga sama dengan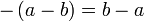

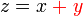
).png)
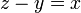
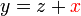
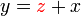
%2bx).png)
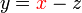
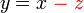
).png)
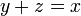
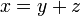
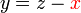
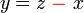
).png)
%3dzovalbox(-x)).png)