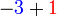Tambah/Tolak Nombor
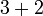
- Bagaimanakah kita wakili ini dalam garis nombor?
- Tambah
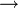
- Tolak
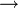
Tolak Nombor
-
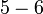 dan
dan 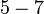
Perhatikan
Nombor Negatif/Positif
Melihat contoh di atas
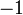 bermaksud
bermaksud 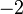 bermaksud
bermaksud
Iaitu boleh ditulis sebagai
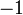
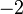
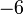
- Perhatikan nombor negatif berkait rapat dengan operasi tolak, dan mungkin sebab itu tanda yang dipilih adalah sama juga dengan tanda tolak.
Oleh kerana kita telah menamakan nombor yang kurang dari 0 sebagai negatif, dan diberi tanda " " bagaimana pula dengan nombor-nombor "biasa" (yang lebih besar dari 0)?
" bagaimana pula dengan nombor-nombor "biasa" (yang lebih besar dari 0)?
Garis Nombor (dengan negatif)
Oleh kerana kita tahu sekarang garis nombor mempunyai sebelah kanan
Bermula dengan Nombor Negatif
Pelbagai Kes
Cuba bandingkan kes-kes berlainan
- a)
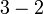
- b)
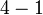
- c)
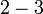
- d)
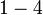
Apakah perbezaan antara a) dan b) dengan c) dan d)?
- e)
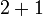
- f)
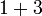
- g)
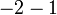
- h)
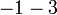
Apakah perbezaan antara e) dan f) dengan g) dan h)?
- i)
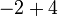
- j)
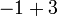
- k)
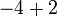
- l)
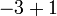
Apakah perbezaan antara i) dan j) dengan k) dan l)?
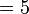
.png)

(3-2(-1)).png)
(3-2nored).png)
(3-2).png)
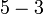
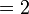
(5-3).png)
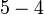
(5-4).png)
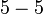
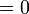
(5-5).png)
(5-6).png)
(5-7).png)
(5-6).png)
(5-7).png)
(5-6).png)
(5-7).png)
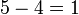 , iaitu 1 di kanan 0, yang juga bermaksud
, iaitu 1 di kanan 0, yang juga bermaksud 
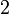
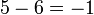
(5-6).png)
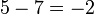
(5-7).png)
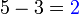
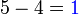
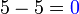
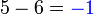
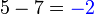
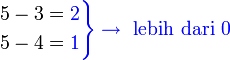
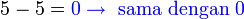
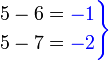
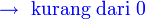
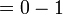
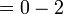
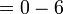
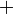 ". Walaubagaimanapun, tanda "
". Walaubagaimanapun, tanda "
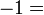
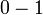 , iaitu
, iaitu 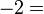
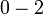 , iaitu
, iaitu 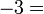
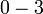 , iaitu
, iaitu 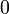 ke
ke 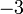 , nilai adalah semakin
, nilai adalah semakin 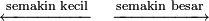
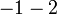
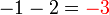
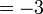
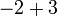
(-2%2b3).png)
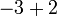
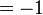
(-3%2b2).png)
(3-2).png)
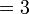
(4-1).png)
(2-3).png)
(1-4).png)
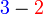 b)
b) 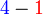
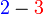 d)
d) 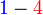
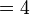
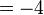
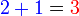 f)
f) 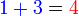 adalah
adalah 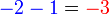 h)
h) 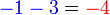 adalah
adalah (-2%2b4).png)
(-1%2b3).png)
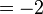
(-4%2b2).png)
(-3%2b1).png)
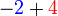 j)
j) 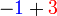
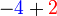 l)
l)