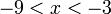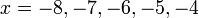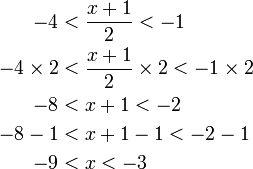Di antara dua nombor
Bagaimanakah kita mewakili
-
 lebih besar daripada
lebih besar daripada 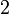 tetapi kurang dari
tetapi kurang dari 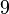 ?
?
Tuliskan ketaksamaan yang diwakili garis nombor berikut
Gabungan Ketaksamaan
Gabungkan ketaksamaan berikut dan senaraikan semua integer  yang memuaskan kedua-dua ketaksamaan berikut
yang memuaskan kedua-dua ketaksamaan berikut
Bentuk lain
Perhatian :
- Bentuk - bentuk ini tidak diuji pada peperiksaan pada tahap ini. Hanya sebagai rujukan. Jika menemui bentuk ini dalam jalan kerja kamu, kemungkinan besar ada kesilapan yang telah dibuat semasa menyelesaikan ketaksamaan yang asal.
Contoh
- Senaraikan semua integer
 yang memuaskan kedua-dua ketaksamaan berikut
yang memuaskan kedua-dua ketaksamaan berikut
-
- Senaraikan semua integer
 yang memuaskan kedua-dua ketaksamaan berikut
yang memuaskan kedua-dua ketaksamaan berikut
-
Latihan 4
I) Senaraikan semua integer  yang memuaskan kedua-dua ketaksamaan berikut
yang memuaskan kedua-dua ketaksamaan berikut
- a)
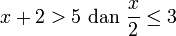
- Jwp :
- Peny :
- b)
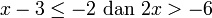
- Jwp :
- Peny :
- c)

- Jwp :
- Peny :
- d)
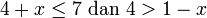
- Jwp :
- Peny :
- e)
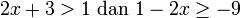
- Jwp :
- Peny :
- f)
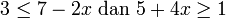
- Jwp :
- Peny :
- g)
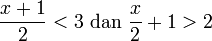
- Jwp :
- Peny :
- h)
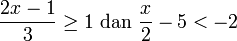
- Jwp :
- Peny :
II) Senaraikan semua integer  yang memuaskan
yang memuaskan
- a)
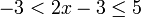
- Jwp :
- Peny :
- b)
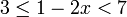
- Jwp :
- Peny :
- c)
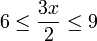
- Jwp :
- Peny :
- d)
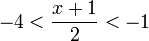
- Jwp :
- Peny :
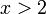
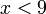

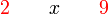
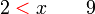 kerana
kerana 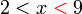

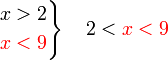
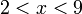 diterima
diterima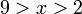 TIDAK diterima sebagai jawapan akhir (walaupun maklumatnya betul)
TIDAK diterima sebagai jawapan akhir (walaupun maklumatnya betul)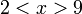 dan
dan 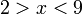 adalah salah sama sekali
adalah salah sama sekali
.png)
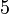 , jadi
, jadi 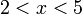
.png)
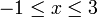
.png)
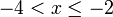
.png)
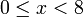
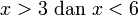
.png)
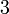 di kanan sebab lebih kecil dari
di kanan sebab lebih kecil dari 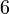
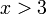
.png)
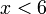 di atas sedikit
di atas sedikit
.png)
.png)
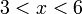
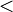 ataupun
ataupun 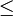 )
)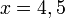
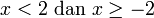
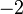 di kiri sebab lebih kecil
di kiri sebab lebih kecil
.png)
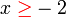
.png)
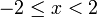
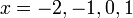
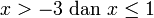
.png)
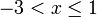
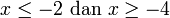
.png)
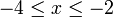
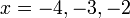
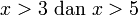
.png)
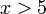
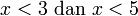
.png)
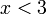
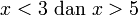
.png)
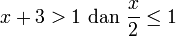
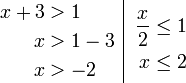
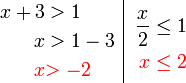
.png)
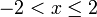
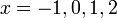
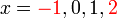
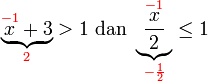
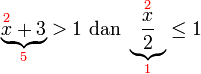

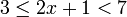



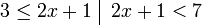
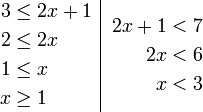
.png)
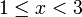
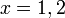
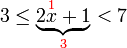
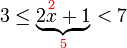
 , kita
, kita 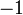 kepada ketiga-tiga "belah" ketaksamaan
kepada ketiga-tiga "belah" ketaksamaan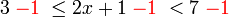
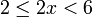
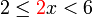 , bahagi
, bahagi 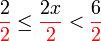

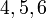
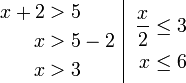
.png)

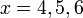
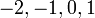
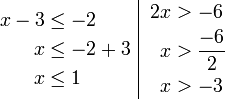
.png)
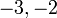
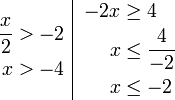
.png)
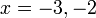
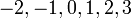
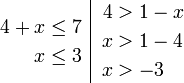
.png)
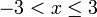
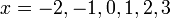
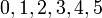
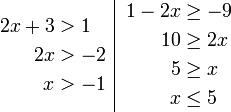
.png)
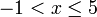
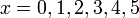
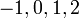
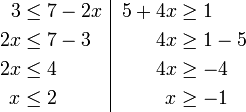
.png)
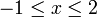
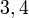

.png)
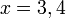
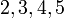
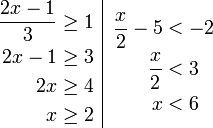
.png)
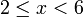
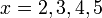
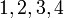
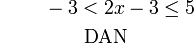
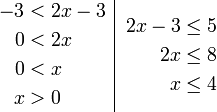
.png)
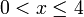
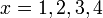
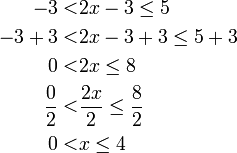
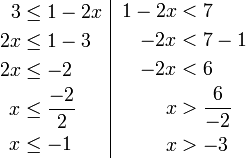
.png)
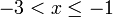
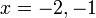
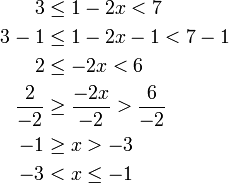
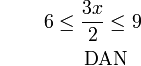
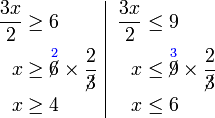
.png)
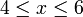
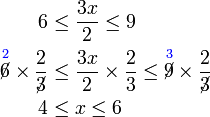
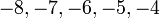
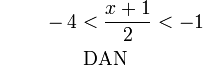
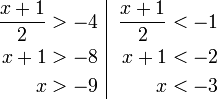
.png)