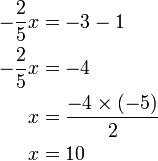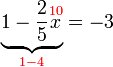Melibatkan Pecahan
Kita boleh gunakan langkah-langkah yang sama untuk menentukan mana yang dipindah dulu
Urutan Operasi
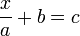
- Jadi, pindahkan
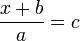
- Jadi, pindahkan
Yang mana boleh darab silang (atas/bawah)
Yang mana boleh pindah (tambah/tolak)
Contoh
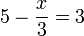
- ATAU
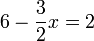
- ATAU
Latihan 15
Selesaikan
- a)
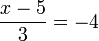
- Jwp :
- Peny :
- b)
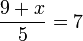
- Jwp :
- Peny :
- c)
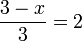
- Jwp :
- Peny :
- d)
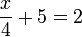
- Jwp :
- Peny :
- e)
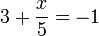
- Jwp :
- Peny :
- f)
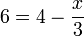
- Jwp :
- Peny :
- g)
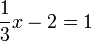
- Jwp :
- Peny :
- h)
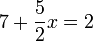
- Jwp :
- Peny :
- i)
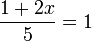
- Jwp :
- Peny :
- j)
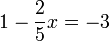
- Jwp :
- Peny :
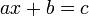
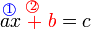
%3dc).png)
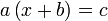
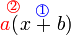
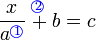
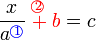
(a)ovalbox(%2bb)%3dc).png)
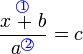
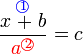
(ovalbox(a))%3dc).png)
redcirc(x%2bb)%3dc).png)
)(redcirc(a))%2bb%3dc).png)
)(redcirc(a))bluecirc(%2bb)%3dc).png)
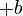 yang "mengacau" jadi kita tidak boleh pindah
yang "mengacau" jadi kita tidak boleh pindah  ke atas
ke atas)(redcirc(a))%3dc.png)
)(redcirc(a))%3dc).png)
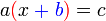 Tidak boleh kerana
Tidak boleh kerana 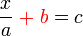
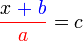
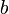 dari kedua-dua belah,
dari kedua-dua belah, 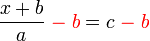
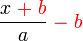 TIDAK menjadi kosong
TIDAK menjadi kosong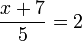
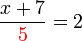 dulu.
dulu. 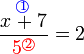
)(ovalbox(5))%3d2.png)
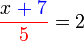
 sebab di dalam pecahan
sebab di dalam pecahan(ovalbox(5))%3d2).png)
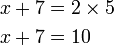
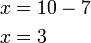
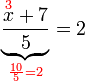
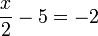
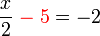 dulu
dulu 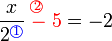
)(ovalbox(2))ovalbox(-5)%3d-2.png)
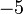 kerana di luar pecahan
kerana di luar pecahan(2)ovalbox(-5)%3d-2).png)
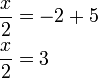
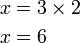
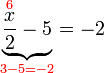
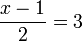
(ovalbox(2))%3d3).png)
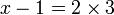
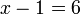
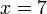
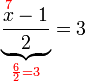
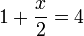
%2bfrac(x)(2)%3d4).png)
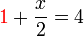 boleh dipindahkan
boleh dipindahkanfrac(ovalbox(x))(ovalbox(2))%3d4.png)
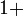 di depan "mengacau"
di depan "mengacau"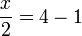
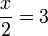
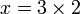
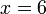
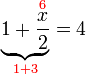
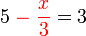 keseluruhannya
keseluruhannya(3))%3dovalbox(%2b3)).png)
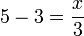
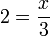
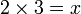
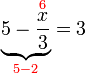
-frac(x)(3)%3d3).png)
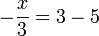
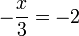
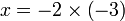
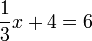
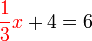 boleh diselesaikan kemudian, yang penting
boleh diselesaikan kemudian, yang penting 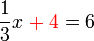 dipindahkan dulu sebab di luar pecahan
dipindahkan dulu sebab di luar pecahan(3)xovalbox(%2b4)%3d6).png)
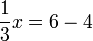
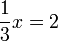
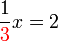
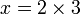
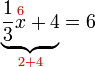
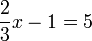
(3)xovalbox(-1)%3d5).png)
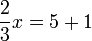
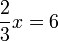
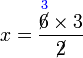
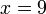
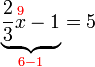
(2)x)%3dovalbox(%2b2)).png)
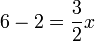
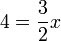
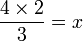
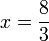
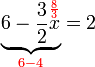
-frac(3)(2)x%3d2).png)
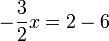
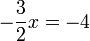
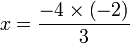
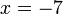
(ovalbox(3))%3d-4).png)
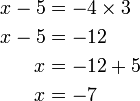
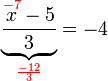
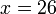
(ovalbox(5))%3d7).png)
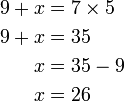
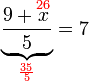
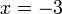
(ovalbox(3))%3d2).png)
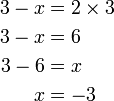
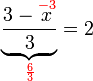
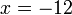
(4)ovalbox(%2b5)%3d2).png)
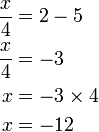
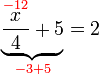
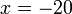
%2bfrac(x)(5)%3d-1).png)
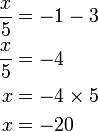
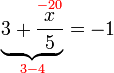
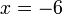
%3d4ovalbox(-frac(x)(3))).png)
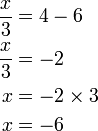
-frac(x)(3)).png)
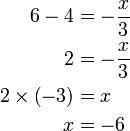
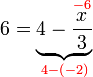
(3)xovalbox(-2)%3d1).png)
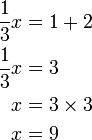
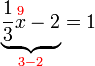
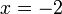
%2bfrac(5)(2)x%3d2).png)
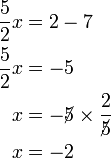
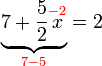
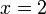
(ovalbox(5))%3d1).png)
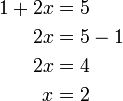
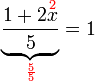
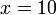
(5)x)%3dovalbox(-3)).png)
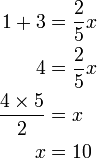
-frac(2)(5)x%3d-3).png)