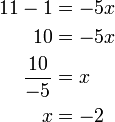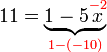Bentuk ax+b=c
Kenapa Cara Berkesan / Tidak Berkesan
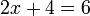
- Kalau pindah
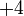 dulu
dulu
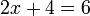
- Kalau pindah
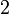 dulu
dulu
Contoh
Bentuk a+bx=c
Urutan Operasi
Yang dipindah dahulu
Contoh
Negatif x
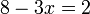
- Cara pertama
Bandingkan

Latihan 13
Selesaikan
- a)
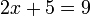
- Jwp :
- Peny :
- b)
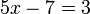
- Jwp :
- Peny :
- c)
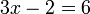
- Jwp :
- Peny :
- d)
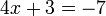
- Jwp :
- Peny :
- e)
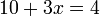
- Jwp :
- Peny :
- f)
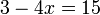
- Jwp :
- Peny :
- g)
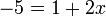
- Jwp :
- Peny :
- h)
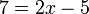
- Jwp :
- Peny :
- i)
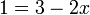
- Jwp :
- Peny :
- j)
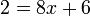
- Jwp :
- Peny :
- k)
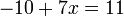
- Jwp :
- Peny :
- l)
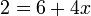
- Jwp :
- Peny :
- m)
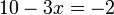
- Jwp :
- Peny :
- n)
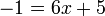
- Jwp :
- Peny :
- o)
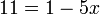
- Jwp :
- Peny :
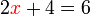
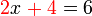
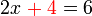 dipindah akan jadi
dipindah akan jadi 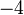
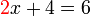 dipindah akan jadi
dipindah akan jadi 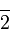 )
)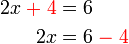 dan
dan 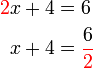 ?
?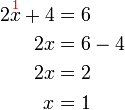
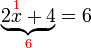
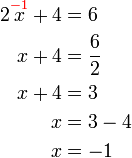
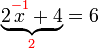
%3d6).png)
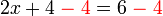
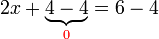
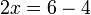
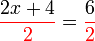
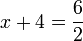 ?
? 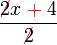 disebabkan
disebabkan 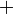
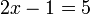
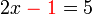 yang ditolak dulu
yang ditolak dulu%3d5).png)
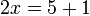
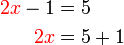 disalin di langkah ini
disalin di langkah ini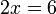
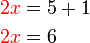
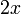 semasa kita mengira sebelah kanan
semasa kita mengira sebelah kanan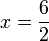
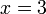
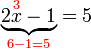
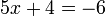
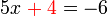 yang ditambah dulu
yang ditambah dulu%3d-6).png)
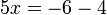
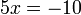 Baru pindahkan yang didarab
Baru pindahkan yang didarab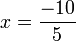
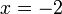
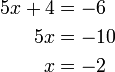
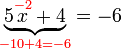 Betul
Betul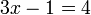
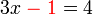 yang ditolak dulu
yang ditolak dulu%3d4).png)
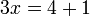
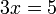
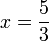
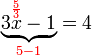
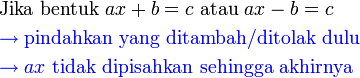
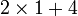
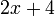
 dulu baru ditambah dalam pengiraan biasa
dulu baru ditambah dalam pengiraan biasa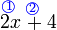
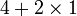
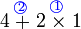
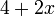
 dalam pengiraan biasa
dalam pengiraan biasa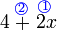
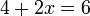
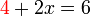 dahulu dan lihat samaada jawapannya betul atau tidak
dahulu dan lihat samaada jawapannya betul atau tidak%2b2x%3d6).png)
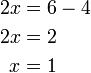
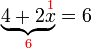
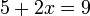
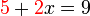 Pindah mana dulu?
Pindah mana dulu?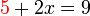 dulu
dulu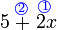

%2b2x%3d9).png)
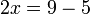
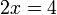
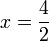
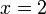
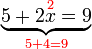
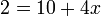
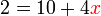 di sebelah kanan tapi ini bukan masalah utama dan boleh diterbalikkan bila-bila masa
di sebelah kanan tapi ini bukan masalah utama dan boleh diterbalikkan bila-bila masa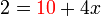 dulu
dulu%2b4x).png)
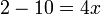
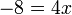
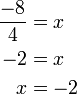
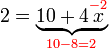

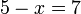
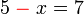 dengan memindah
dengan memindah 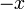 ke sebelah.
ke sebelah.
%3dovalbox(%2b7)5-7%3dx).png)
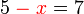 dibiarkan dan sebaliknya pindahkan
dibiarkan dan sebaliknya pindahkan 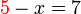 dulu.
dulu.
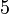 .
.-x%3d7).png)
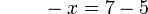
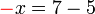 masih ada
masih ada 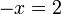
 dan pindahkan secara bahagi ke bawah
dan pindahkan secara bahagi ke bawah
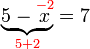
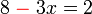 boleh diselesaikan dengan dua cara, iaitu
boleh diselesaikan dengan dua cara, iaitu  ke sebelah supaya menjadi positif
ke sebelah supaya menjadi positif dulu, dan sebaliknya pindahkan
dulu, dan sebaliknya pindahkan 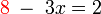 dulu, kemudian baru pindahkan negatif bersama-sama nombor.
dulu, kemudian baru pindahkan negatif bersama-sama nombor.%3dovalbox(%2b2)).png)
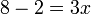
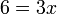
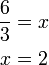
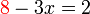 yang dipindah
yang dipindah

-3x%3d2).png)
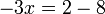
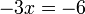
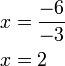
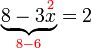
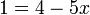
%3d4ovalbox(-5x)).png)
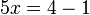
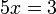
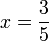
-5x).png)
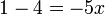
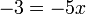
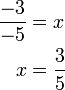
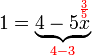
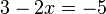
%3dovalbox(-5)).png)

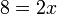
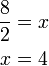
-2x%3d-5).png)
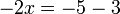
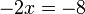
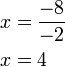
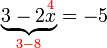

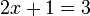
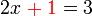 dulu
dulu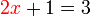 tidak dipisahkan
tidak dipisahkan
%3d3).png)
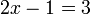
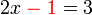 dulu
dulu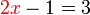 tidak dipisahkan
tidak dipisahkan
%3d3).png)
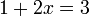
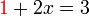 dulu
dulu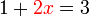 tidak dipisahkan
tidak dipisahkan
%2b2x%3d3).png)
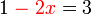 dulu
dulu
%3dovalbox(%2b3)).png)
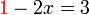 dulu
dulu
-2x%3d3).png)
%3d9).png)
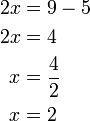
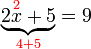
%3d3).png)
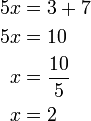
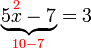
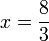
%3d6).png)
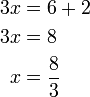
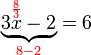
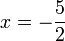
%3d-7).png)
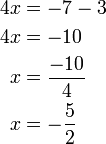
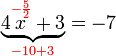
%2b3x%3d4).png)
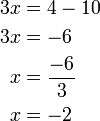
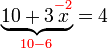
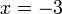
%3dovalbox(%2b15)).png)
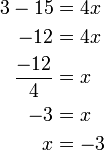
-4x%3d15).png)
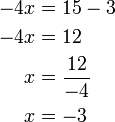
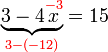
%2b2x).png)
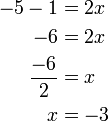
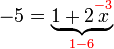
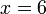
).png)
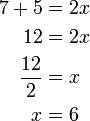
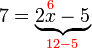
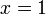
%3d3ovalbox(-2x)).png)
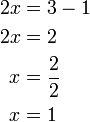
-2x).png)
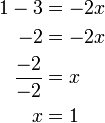
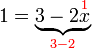
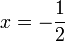
).png)
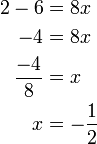
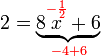
%2b7x%3d11).png)
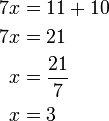
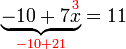
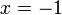
%2b4x).png)
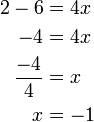
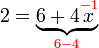

%3dovalbox(-2)).png)
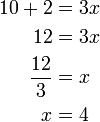
-3x%3d-2).png)
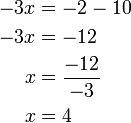
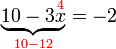
).png)
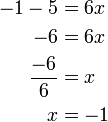
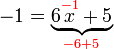
%3d1ovalbox(-5x)).png)
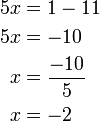
-5x).png)