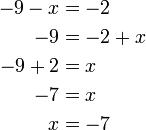Nombor tolak x (negatif x)
Lebih banyak Contoh
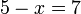
- atau dalam dua langkah
Latihan 3
Selesaikan
- a)
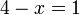
- Jwp :
- Peny :
- b)
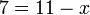
- Jwp :
- Peny :
- c)
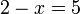
- Jwp :
- Peny :
- d)
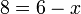
- Jwp :
- Peny :
- e)
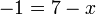
- Jwp :
- Peny :
- f)
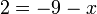
- Jwp :
- Peny :
- g)
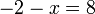
- Jwp :
- Peny :
- h)
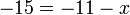
- Jwp :
- Peny :
- i)
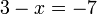
- Jwp :
- Peny :
- j)
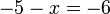
- Jwp :
- Peny :
- k)
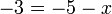
- Jwp :
- Peny :
- l)
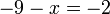
- Jwp :
- Peny :
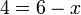
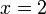 , kerana
, kerana 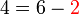
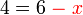 ada tanda tolak/negatif di depan
ada tanda tolak/negatif di depan 
).png)

%2bx%3d6x%3d6-4).png)
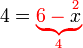
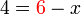 BUKAN masalah utama kerana
BUKAN masalah utama kerana  tetap masih ada pada
tetap masih ada pada 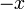

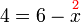

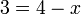
).png)
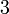 ke sebelah kanan.
ke sebelah kanan.%3d4ovalbox(-x)).png)
%3d4ovalbox(-x)x%3d4-3).png)
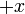 , tapi
, tapi 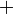 tidak perlu ditulis kerana kita akan memindahkan
tidak perlu ditulis kerana kita akan memindahkan 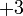 (+ itu kita tambah sendiri) dipindah menjadi
(+ itu kita tambah sendiri) dipindah menjadi 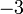 di sebelah
di sebelah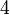 disalin
disalin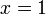
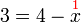
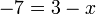
%3d3ovalbox(-x)x%3d3%2b7).png)
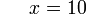
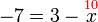
).png)
%2bx%3d3x%3d3%2b7).png)

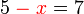 , jadi perlu kita
, jadi perlu kita %3dovalbox(%2b7)5-7%3dx).png)
%3d7).png)
%2bx5-7%3dx).png)
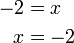 atau terus
atau terus 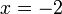
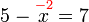
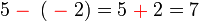
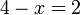
%3dovalbox(%2b2)4-2%3dx).png)
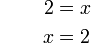
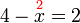
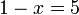
%3dovalbox(%2b5)1-5%3dx).png)
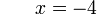
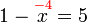
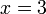
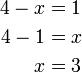 atau
atau 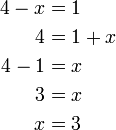
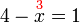

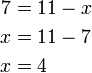 atau
atau 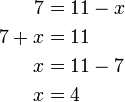
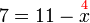
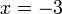
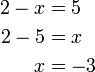 atau
atau 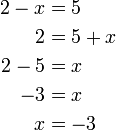
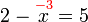
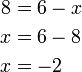 atau
atau 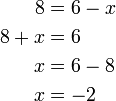
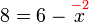
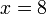
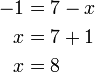 atau
atau 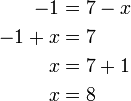
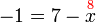
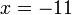
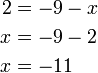 atau
atau 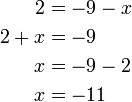
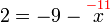
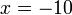
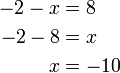 atau
atau 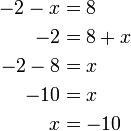
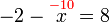
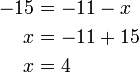 atau
atau 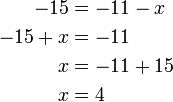
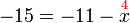
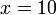
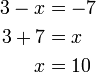 atau
atau 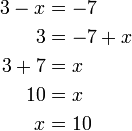
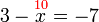
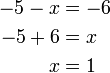 atau
atau 
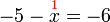
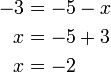 atau
atau 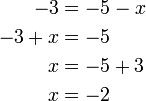
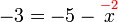
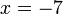
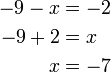 atau
atau