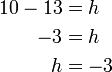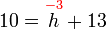Cuba
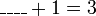
- Kita perlukan satu nombor yang bila ditambah dengan 1 akan menjadi 3. Apakah nombor tersebut?
-
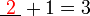
- Analisis
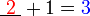
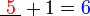
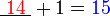
- Kita perlu cari nombor yang bila ditambah 1 akan jadi nombor di kanan. Jadi, berbanding dengan nombor di kanan, nombor itu mesti kurang 1. Jadi, nombor itu juga boleh dicari dengan menolak 1 dari nombor di kanan.
-
-
Sekarang kita lihat kes untuk nombor lain
- Cuba kita tengok hubungan nombor yang diperlukan dengan nombor-nombor yang sedia ada
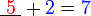
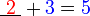
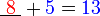
- Kita nampak di sini bahawa nombor yang diperlukan sama dengan nombor-nombor asal ditolak (nombor di kanan ditolak nombor yang asalnya ditambah)
-
-
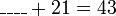
- Dari contoh atas, jawapannya sama dengan
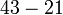 iaitu
iaitu 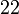
- Kita boleh pastikan samaada jawapan ini betul atau tidak dengan mengira
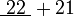 sememangnya
sememangnya 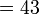
- Dari contoh atas, jawapannya sama dengan
Cara Pantas
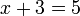
- Dari contoh atas kita tahu bahawa nilai
 akan diberikan oleh
akan diberikan oleh 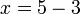 , iaitu
, iaitu 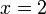 , suatu jawapan yang kita pasti betul kerana akan betul bila diganti balik ke dalam persamaan.
, suatu jawapan yang kita pasti betul kerana akan betul bila diganti balik ke dalam persamaan. - Mari kita teliti cara yang digunakan disini.
-
- Dari contoh atas kita tahu bahawa nilai
- Perhatikan apa terjadi kepada nombor yang ditambah
 masih ditengah-tengah
masih ditengah-tengah
 masih di tengah
masih di tengah
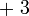 menjadi
menjadi 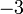 selepas dipindah ke kanan
selepas dipindah ke kanan
- Jawapan perlu memenuhi persamaan yang diberikan / betul bila diganti ke dalam persamaan
-
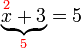 Sememangnya betul.
Sememangnya betul.

Sebab Cara Pantas Berkesan
- Mari kita lihat kenapa cara ini boleh digunakan.
- Sebelum itu, ingat kembali bahawa bila kita manipulasi persamaan :
- Apa saja yang dibuat kepada satu belah mesti juga dibuat kepada sebelah yang lain
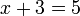
- Kita perlu cari
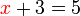 sahaja, jadi perlu cari satu jalan untuk hapuskan
sahaja, jadi perlu cari satu jalan untuk hapuskan 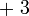 dari sebelah kiri.
dari sebelah kiri. - Bagaimana
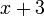 boleh bertukar kepada
boleh bertukar kepada  sahaja?
sahaja? 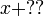 yang akan jadi balik
yang akan jadi balik  sahaja?
sahaja? 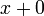
- Jadi kita perlu tukar
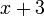 kepada
kepada 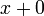 , iaitu tukarkan
, iaitu tukarkan 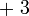 kepada
kepada 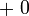
- Bagaimanakah
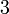 akan jadi
akan jadi 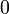 ? dengan menolak
? dengan menolak 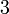
-
- Kita perlu cari
- Tapi kita tidak boleh dengan tiba-tiba menolak dari satu belah sahaja. Mesti juga tolak sebelah kiri
-
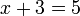
- Kita akan tolak 3 dari kedua-dua belah
- Dimanakah tanda
 ? Masih di tengah. Ada di depan? Tiada. Ingat, persamaan baru tidak lagi sama dengan yang asal, hanya sebelah kiri baru sama dengan sebelah kanan baru.
? Masih di tengah. Ada di depan? Tiada. Ingat, persamaan baru tidak lagi sama dengan yang asal, hanya sebelah kiri baru sama dengan sebelah kanan baru.
- Dimanakah tanda
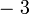 ? Untuk hapuskan
? Untuk hapuskan 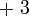 yang "mengacau"
yang "mengacau" 
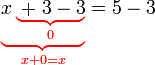
- Jadi memang sah terhapus
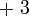 dan hanya tinggal
dan hanya tinggal  di sebelah kiri
di sebelah kiri
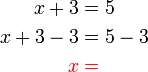
- Untuk tujuan kita di sini, salin dulu sebelah kanan
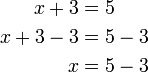
- berbanding
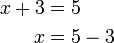
- Kita akan nampak bahawa
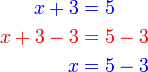
- berbanding
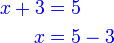
- Sebenarnya sama, hanya dalam cara pantas kita melangkah terus ke baris ketiga
- Tanda
 ditengah dan bukannya di depan
ditengah dan bukannya di depan
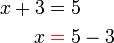
- dan bukannya
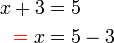
- Ini kerana bila kita memanipulasi persamaan, yang lama TIDAK sama dengan yang baru, jadi bila kita pindah, tanda
 masih hanya ditulis ditengah.
masih hanya ditulis ditengah.
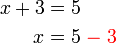
- dan bukannya terus
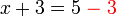
- Ini kerana bila kita memanipulasi persamaan, sebelah kiri/kanan yang baru kena ditulis di baris seterusnya, jadi bila kita memindah, juga perlu tulis di baris seterusnya.
Contoh
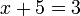
- Lepas dipindah, adakah akan menjadi
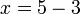 atau
atau 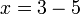 ?
?- Ingat, kita akan tahu sama jawapannya betul atau tidak dengan menganti balik ke dalam persamaan
- Jika
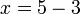
-
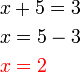
- Ganti balik dalam persamaan untuk semak
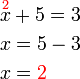
- Boleh kita terus tulis jawapan di atas persamaan asal untuk semak dengan cepat
- SALAH
-
- Lepas dipindah, adakah akan menjadi
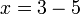
-
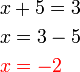
- Ganti balik dalam persamaan untuk semak
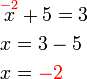
- BETUL
- Ambil tanda di depan, BUKAN belakang
- Perhatikan juga
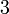 perlu disalin ke bawah dan tidak berubah tanda-nya
perlu disalin ke bawah dan tidak berubah tanda-nya
- Perhatikan juga tidak semestinya besar tolak kecil, yang penting adalah tengok mana yang dipindah dan mana yang disalin
Cuba yang di bawah
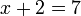
- Pindahkan (di baris seterusnya), tambah jadi tolak, tanda masih di depan
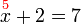 Betul.
Betul.

Lebih banyak Contoh
Contoh (x di sebelah kanan)
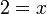
- Jika
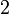 adalah sama dengan
adalah sama dengan  , jadi secara logiknya
, jadi secara logiknya  sama dengan 2
sama dengan 2 - Kita perlu tulis
 di kiri sebagai jawapan akhir, jadi kita perlu tulis semula sebagai
di kiri sebagai jawapan akhir, jadi kita perlu tulis semula sebagai
-
- Jika
- Perhatikan
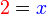
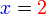
- Kita sedang menerbalikkan persamaan
- Sebelah kanan jadi sebelah kiri, sebelah kiri menjadi sebelah kanan
- Kenapa
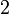 tidak bertukar kepada
tidak bertukar kepada 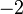 ? Kita di sini bukan memindah, tetapi menerbalikkan persamaan. Iaitu kita salin sebelah kiri ke kanan, dan kanan ke kiri, jadi memanglah tiada perubahan tanda di sini.
? Kita di sini bukan memindah, tetapi menerbalikkan persamaan. Iaitu kita salin sebelah kiri ke kanan, dan kanan ke kiri, jadi memanglah tiada perubahan tanda di sini.
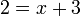
- Perhatikan

- ada dua perkara yang perlu dilakukan
- Paling baik kita buat satu-per-satu
- Pindahkan
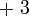
- Sebenarnya boleh juga pindah ke depan tetapi kita perlu letak
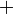 pada
pada 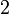
- Pindahkan
- Perhatikan
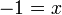
- Selesai? Tidak,
 perlu ditulis di kiri pada akhirnya.
perlu ditulis di kiri pada akhirnya.
- Kita juga boleh selesaikan masalah
 di sebelah kanan dulu.
di sebelah kanan dulu. - Terbalikkan (tiada perubahan tanda, salin bulat-bulat)
 di sebelah kanan bukan masalah besar, jadi paling baik guna cara pertama, iaitu tinggalkan
di sebelah kanan bukan masalah besar, jadi paling baik guna cara pertama, iaitu tinggalkan  di sebelah kanan dulu sehingga langkah terakhir.
di sebelah kanan dulu sehingga langkah terakhir.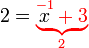 Betul.
Betul.
- Analisa
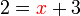 di sebelah kanan tetapi bukan masalah besar, biarkan dulu
di sebelah kanan tetapi bukan masalah besar, biarkan dulu
 dulu
dulu
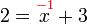 Betul.
Betul.

Lebih banyak Contoh
Contoh (x di belakang)
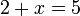
- Apakah jawapan yang sepatutnya?
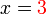 kerana
kerana 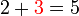
- Apakah jawapan yang sepatutnya?
- Mari kita lihat cara memindah
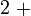 ? Tidak. Kerana kita perlukan tanda di depan
? Tidak. Kerana kita perlukan tanda di depan- Nombor yang tiada tanda di depan maksudnya positif atau negatif? Positif/tambah. Selepas dipindah, ianya akan jadi tolak. Jadi, sebagai peringatan, kita letakkan tanda positif ini di depan, kemudian baru dipindahkan.
%2bx%3d5x%3d5-2).png)
- Apakah yang terjadi kepada tanda
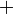 di depan
di depan  ?
?
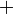 itu tidak ditulis sebab tidak diperlukan untuk ditulis, bukan sebab dipindah.
itu tidak ditulis sebab tidak diperlukan untuk ditulis, bukan sebab dipindah.
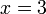
 Betul
Betul- Mari kita lihat apa akan berlaku jika kita ambil
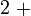 dan tukar kepada
dan tukar kepada 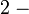 lepas dipindah.
lepas dipindah.
- Adalah SALAH kerana
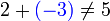
- Mengapakah cara begitu tidak berhasil?
- Jika kita cuba meletakkan
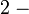 di kedua-dua belah persamaan, kita sebenarnya akan dapat
di kedua-dua belah persamaan, kita sebenarnya akan dapat 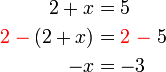
- dan bukannnya
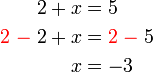
- Jika kita cuba meletakkan
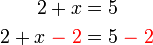
- Ingat bahawa bila kita nak mengira
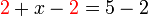
- tanda yang dilihat ialah
- Tanda DEPAN
- dan bukannya
- Tanda DEPAN
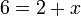
- Pindahkan ke belakang nombor yang sudah sedia ada
 di kiri
di kiri
 di kiri dulu baru kirakan.
di kiri dulu baru kirakan.- Semak:
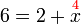 Betul
Betul
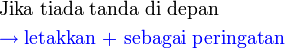
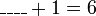
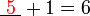
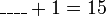
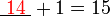
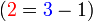
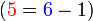
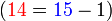
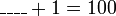
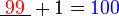
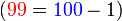
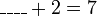
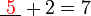
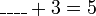
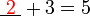
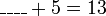
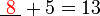
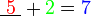
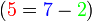
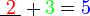
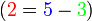
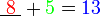
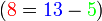
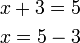
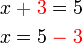
 seakan-akan
seakan-akan 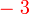
%3d5).png)
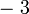 TIDAK ditulis di sini tetapi BARIS SETERUSNYA
TIDAK ditulis di sini tetapi BARIS SETERUSNYA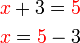
%3d5downarrowdownarrowx%3d5-3).png)
%3d5downarrowdownarrowx%3d5-3LHSRHS).png)
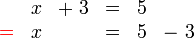 adalah SALAH.
adalah SALAH.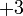 dan anak panah untuk pindahkan ke sebelah yang lain, tapi JANGAN tulis di baris ini.
dan anak panah untuk pindahkan ke sebelah yang lain, tapi JANGAN tulis di baris ini.%3d5%3d).png)
%3d5%3d-3).png)

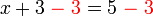
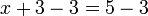
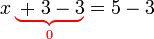
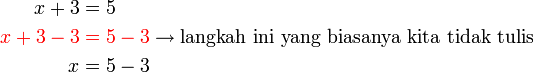
%3d3downarrowdownarrowx%3d3-5).png)
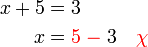
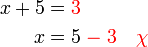
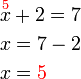

%3d7).png)
%3d7%3d).png)
%3d7%3d-2).png)
%3d7downarrowdownarrowx%3d7-2).png)

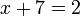
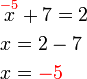
%3d2).png)
%3d2%3d).png)
%3d2%3d-7).png)
%3d2downarrowdownarrowx%3d2-7).png)
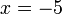
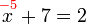 Betul.
Betul.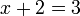
%3d3x%3d3-2).png)

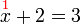
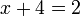
%3d2x%3d2-4).png)

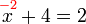
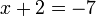
%3d-7x%3d-7-2).png)

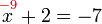
).png)
(2%3dxovalbox(%2b3)).png)
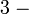
2-3%3dx).png)
-3%2b2%3dx).png)
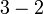
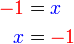
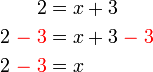
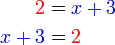
%3d2x%3d2-3).png)
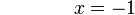
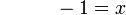
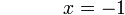
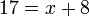
17-8%3dx).png)
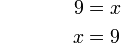
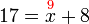
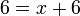
6-6%3dx).png)
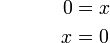
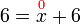
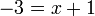
-3-1%3dx).png)
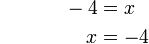
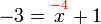

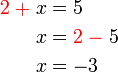
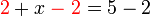
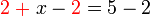
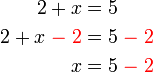
%2bx6-2%3dx).png)
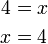
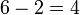 dalam minda, tapi terus letak di kanan
dalam minda, tapi terus letak di kanan
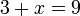
%2bx%3d9x%3d9-3).png)

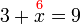
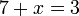
%2bx%3d3x%3d3-7).png)

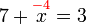
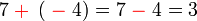
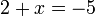
%2bx%3d-5x%3d-5-2).png)

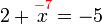
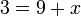
%2bx3-9%3dx).png)
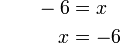
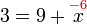
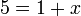
%2bx5-1%3dx).png)
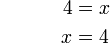
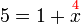
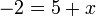
%2bx-2-5%3dx).png)
%3d5).png)
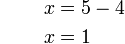
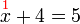
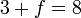
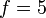
%2bf%3d8).png)
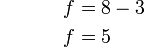
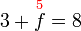
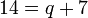
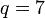
).png)
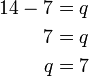
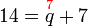
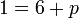
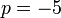
%2bp).png)
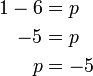
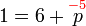
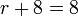
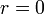
%3d8).png)
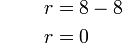
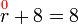
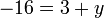
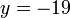
%2by).png)
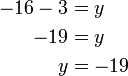
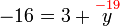
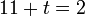
%2bt%3d2).png)
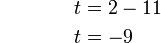
).png)
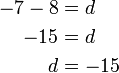
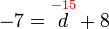
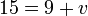
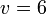
%2bv).png)
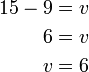
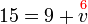
%3d-3).png)
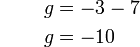
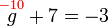
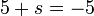
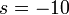
%2bs%3d-5).png)
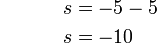
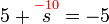
).png)