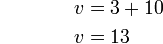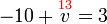Cuba
- Analisis
Sekarang kita lihat kes untuk nombor lain
- Cuba kita tengok hubungan nombor yang diperlukan dengan nombor-nombor yang sedia ada
Cara Pantas
Sebab Cara Pantas Berkesan
Lebih banyak Contoh
Latihan 2
Selesaikan
- a)
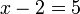
- Jwp :
- Peny :
- b)
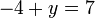
- Jwp :
- Peny :
- c)
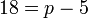
- Jwp :
- Peny :
- d)
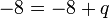
- Jwp :
- Peny :
- e)
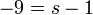
- Jwp :
- Peny :
- f)
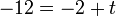
- Jwp :
- Peny :
- g)
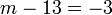
- Jwp :
- Peny :
- h)
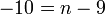
- Jwp :
- Peny :
- i)
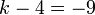
- Jwp :
- Peny :
- j)
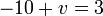
- Jwp :
- Peny :
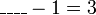
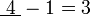
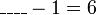
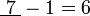
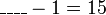
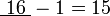
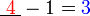
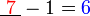
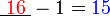
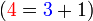
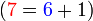
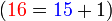
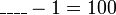
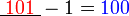
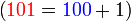
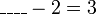
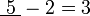
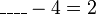
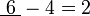
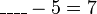

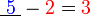
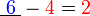
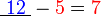
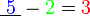
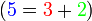
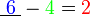
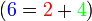
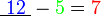
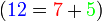
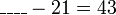
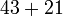 iaitu
iaitu 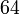
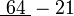 sememangnya
sememangnya 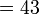
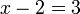

%3d3).png)
%3d3x%3d3%2b2).png)

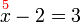
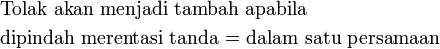
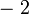 , kita
, kita 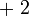 , di
, di 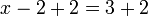
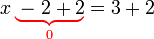
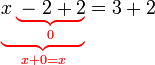
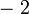 dan hanya tinggal
dan hanya tinggal  di sebelah kiri
di sebelah kiri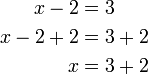
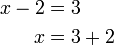
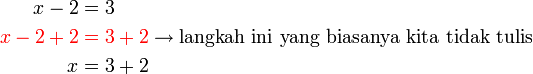
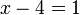
%3d1x%3d1%2b4).png)

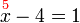
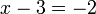
%3d-2x%3d-2%2b3).png)

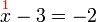
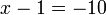
%3d-10x%3d-10%2b1).png)

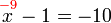
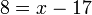
8%2b17%3dx).png)
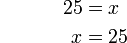
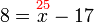
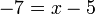
-7%2b5%3dx).png)
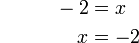
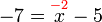
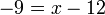
-9%2b12%3dx).png)
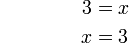
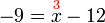
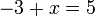
%2bx%3d5x%3d5%2b3).png)

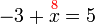
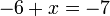
%2bx%3d-7x%3d-7%2b6).png)

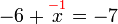
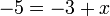
%2bx-5%2b3%3dx).png)
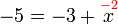
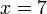
%3d5).png)
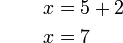
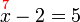
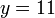
%2by%3d7).png)
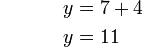
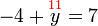
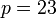
.png)
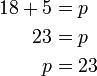
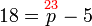
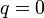
%2bq).png)
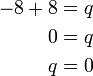
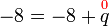
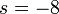
.png)
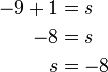
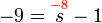
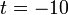
%2bt).png)
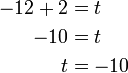
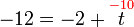
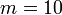
%3d-3).png)
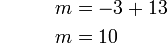
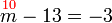
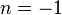
.png)
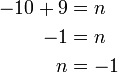
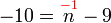
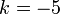
%3d-9).png)
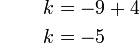
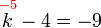
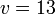
%2bv%3d3).png)