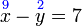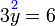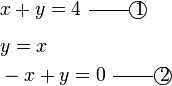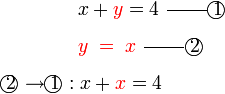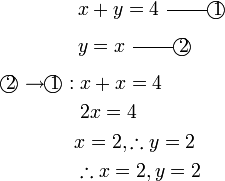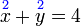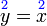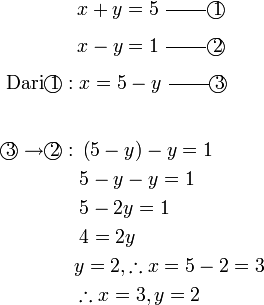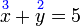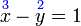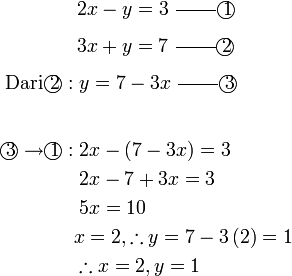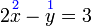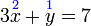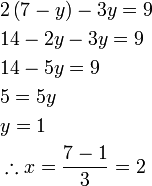Last modified on 18 November 2015, at 08:24

PT3 2016 : Persamaan Linear Serentak (Kaedah Penggantian)

Cara Penggantian

  • a)
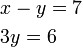
    • Perhatikan
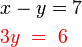
      • Hanya ada satu pembolehubah, jadi boleh terus selesaikan. Lepas itu, ganti untuk selesaikan yang satu lagi.
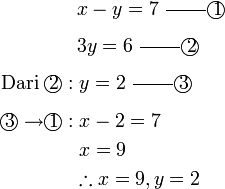
      • Semak
    • Dalam erti kata lain, walaupun nampak 2 persamaan, tidak semestinya bermaksud mesti buat cara panjang. Kalau ada satu persamaan hanya mempunyai satu pembolehubah, itu yang diselesaikan dulu.


  • b)
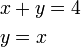
    • Kedua-dua persamaan mempunyai dua pembolehubah. Perhatikan pembolehubah tidak tersusun
    • Untuk kaedah penghapusan, perlulah susun semula
    • Untuk kaedah alternatif
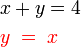
      • adalah seperti 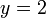, yang kita boleh gantikan ke dalam persamaan yang satu lagi
    • Kelebihan di sini, ialah selepas selesai boleh terus dapat nilai 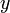( kerana )
    • Semak


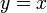  • c)
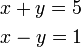
  • Soalan sebegini sememangya lebih senang diselesaikan dengan penghapusan, tetapi kita boleh juga guna cara penggantian
    • Yang paling penting (tidak kira cara) adalah menyemak jawapan pada akhirnya
    • Dari contoh di atas, kita nampak kita boleh menggantikan sekiranya salah satu persamaan dalam bentuk
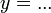      • iaitu 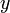adalah salah satu pembolehubah dalam sebutan pembolehubah yang lain
      • Cara ini berkesan kerana selepas persamaan ini digantikan ke persamaan lain, akan hilang pembolehubah ini
        • Ingat bahawa yang paling penting dalam penyelesaian persamaan serentak adalah untuk menghapuskan salah satu pembolehubah supaya boleh diselesaikan yang satu lagi
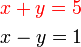
    • Melihat soalannya, tiada persamaan yang sudah dalam bentuk yang dikehendaki. Jadi kita ambil
      • Untuk disusun semula, supaya satu pembolehubah menjadi subjek
      • atau  ??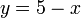
      • kedua-duanya pun boleh. Kita teruskan dengan menggunakan yang pertama
    • Semak (pada persamaan-persamaan ASAL)


  • c)
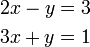
    • Yang manakah cara paling baik untuk susun semula untuk gantikan?
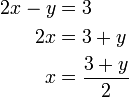
      • atau
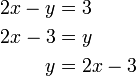
      • atau
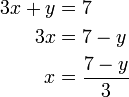
      • atau
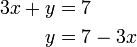
    • Cara terakhir ialah yang paling senang. Yang melibatkan pecahan akan merumitkan pengiraan.
    • Semak (pada persamaa-persamaan ASAL)
  • ATAU
    • Kita lihat apa yang berlaku jika kita memilih yang mempunyai pecahan
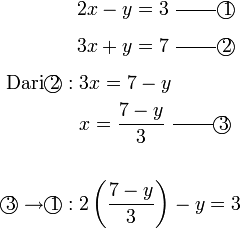
    • Samaada kita hapuskan pecahan dengan mendarab 3
    • Atau gabungkan pecahan dahulu
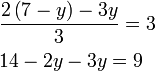
      • dan langkah seterusnya adalah sama
    • Kita melihat pengiraan menjadi rumit dengan adanya pecahan. Jadi jika boleh elakkan. Dan kebanyakkan soalan lebih sesuai menggunakan kaedah penghapusan

Pilih kaedah yang sesuai untuk menyelesaikan persamaan serentak berikut

  • a)
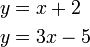
  • Melihat cara persamaan telah disusun
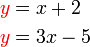
    • Lebih senang terus guna penggantian
    • Jika guna penghapusan, paling baik susun semula


  • b)
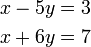
  • Cara penghapusan. Tiada sebabnya kita gunakan penggantian dalam kes ini.


  • c)
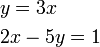
  • Melihat
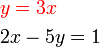
    • Lebih senang terus guna penggantian


  • d)
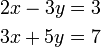
  • Cara penghapusan. Walaupun memerlukan pendaraban kedua-dua persamaan, cara penggantian lagi susah kerana terpaksa melibatkan pecahan