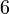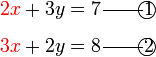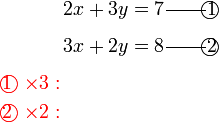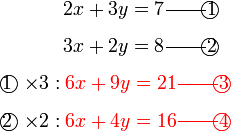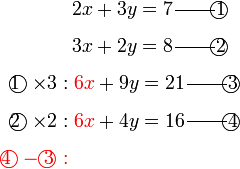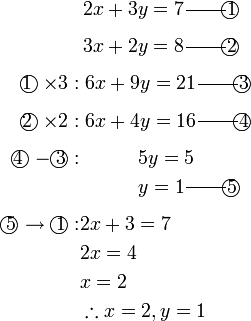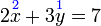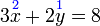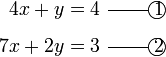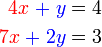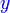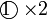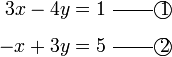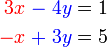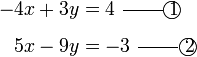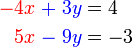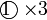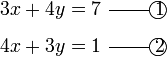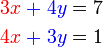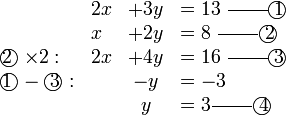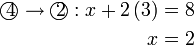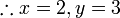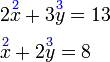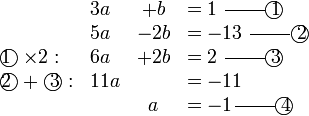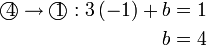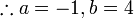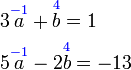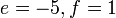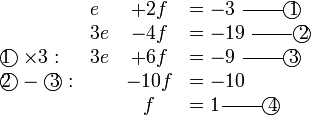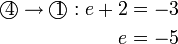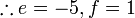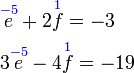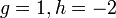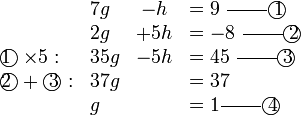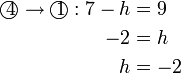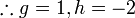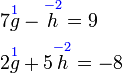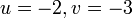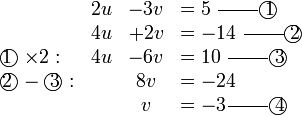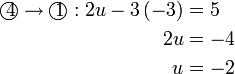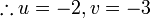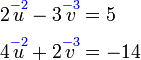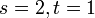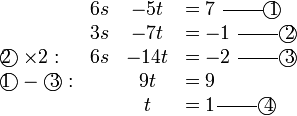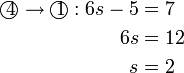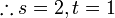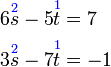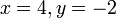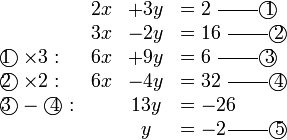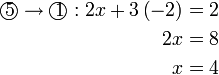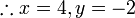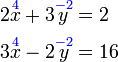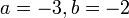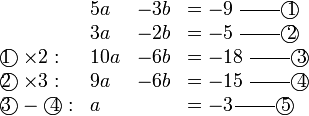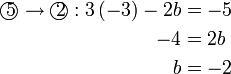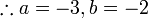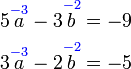Mendarab Persamaan Linear dengan pemalar
Selain daripada operasi tambah/tolak dua persamaan, kita juga boleh buat operasi lain atas persamaan seperti darab/bahagi dengan suatu pemalar/nombor.
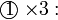
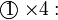
Bahagi dengan Pemalar
- Untuk bahagi, cara sama digunakan
- Perhatikan :
Mendarab untuk menghilangkan pecahan
Contoh
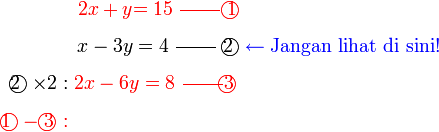
Selesaikan persamaan serentak berikut
Pilih operasi yang perlu dilakukan untuk menghapuskan salah satu pembolehubah
Latihan 2
Selesaikan persamaan serentak berikut
- a)
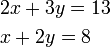
- Jwp :
- Peny :
- b)
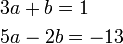
- Jwp :
- Peny :
- c)
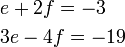
- Jwp :
- Peny :
- d)
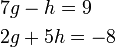
- Jwp :
- Peny :
- e)
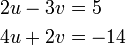
- Jwp :
- Peny :
- f)
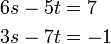
- Jwp :
- Peny :
- g)
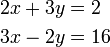
- Jwp :
- Peny :
- h)
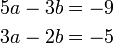
- Jwp :
- Peny :
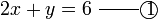
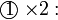
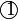 darab dengan 2
darab dengan 2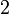 , termasuk nombor di kanan. Mari kita lihat samaada ianya sememangnya begini
, termasuk nombor di kanan. Mari kita lihat samaada ianya sememangnya begini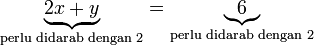
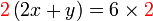
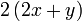
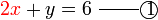
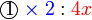
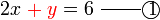
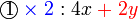
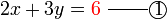
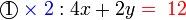
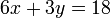
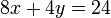
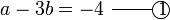
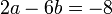
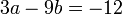
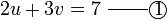
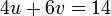
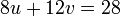

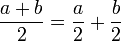
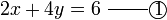
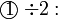
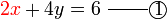
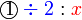
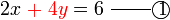
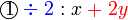
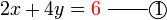
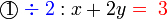
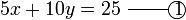
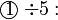
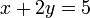
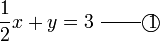
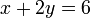
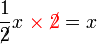
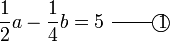
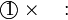
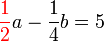 memang akan hilang pecahannya
memang akan hilang pecahannya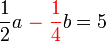 tidak. Ingat bahawa tujuan kita hilangkan pecahan adalah untuk memudahkan pengiraan, jadi perlulah kita hilangkan semuanya.
tidak. Ingat bahawa tujuan kita hilangkan pecahan adalah untuk memudahkan pengiraan, jadi perlulah kita hilangkan semuanya.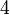 . Kedua-dua akan hilang
. Kedua-dua akan hilang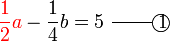
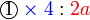
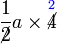
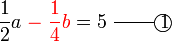
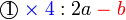
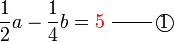
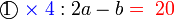
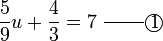
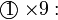
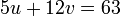
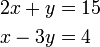
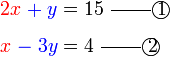

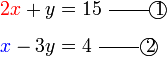
 kepada
kepada 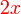 , dan ini boleh dibuat dengan
, dan ini boleh dibuat dengan 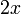 kepada
kepada 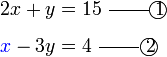
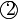 , jadi kita perlu darab
, jadi kita perlu darab 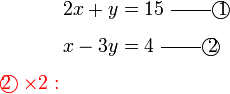
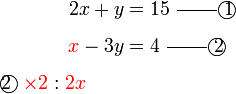
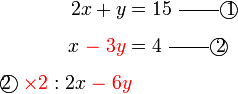
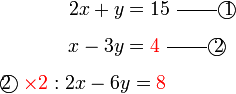
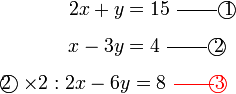
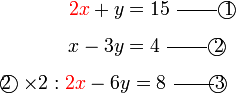
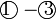
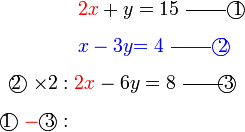
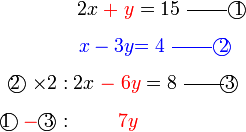
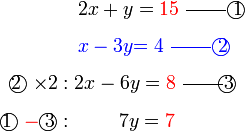
 di bawah sebelum ditolak. Apapun, ingat bahawa segala kesilapan dapat disemak dengan menyemak jawapan akhir
di bawah sebelum ditolak. Apapun, ingat bahawa segala kesilapan dapat disemak dengan menyemak jawapan akhir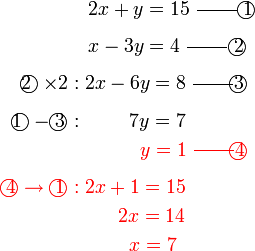
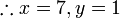
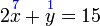
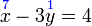
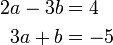
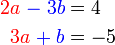
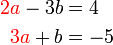 ?
?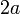 kepada
kepada 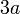 dengan mendarab suatu nombor bulat?
dengan mendarab suatu nombor bulat? 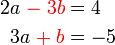
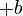 ditukar menjadi yang mempunyai "3" (tak kira positif atau negatif) dengan senang?
ditukar menjadi yang mempunyai "3" (tak kira positif atau negatif) dengan senang? 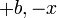 dsb) kerana senang ditukarkan ke apa-apa nombor.
dsb) kerana senang ditukarkan ke apa-apa nombor.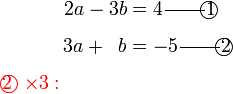
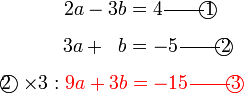
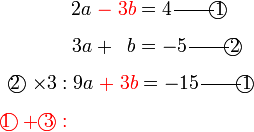
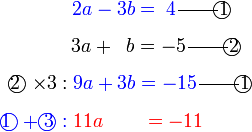
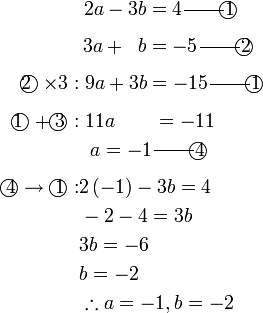
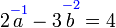
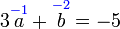
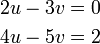
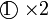
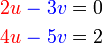
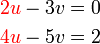
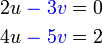
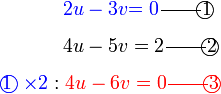
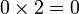
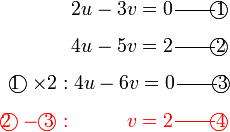
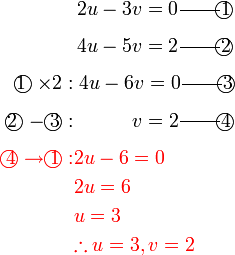
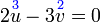
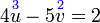
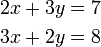
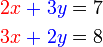

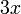 dan sebaliknya. Ingat, tujuan kita adalah menukar supaya ianya sama. Jadi, kalau tukar satu sahaja tidak cukup, kita tukar
dan sebaliknya. Ingat, tujuan kita adalah menukar supaya ianya sama. Jadi, kalau tukar satu sahaja tidak cukup, kita tukar 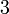 ?
?