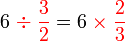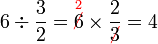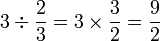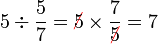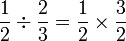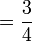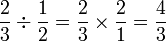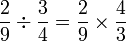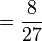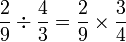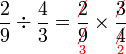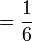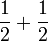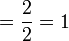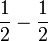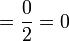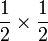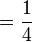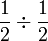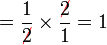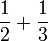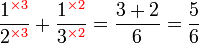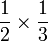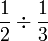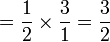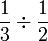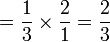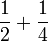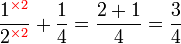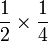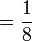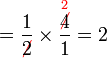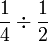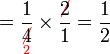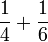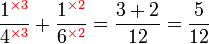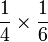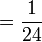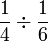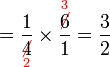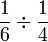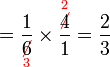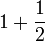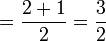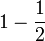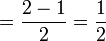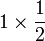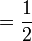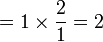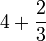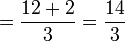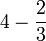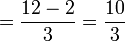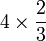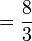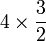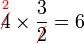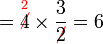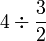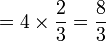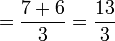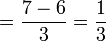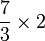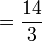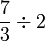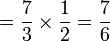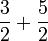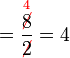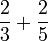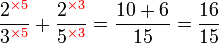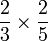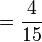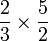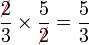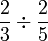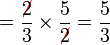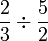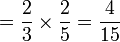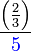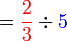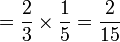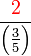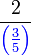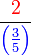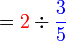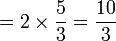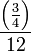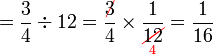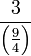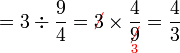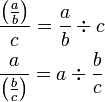Bahagi dengan nombor bulat
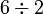
- atau
Bahagi dengan 1/n
Apakah maksud 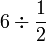 ?
?
Contoh
Dalam setiap kes di atas, didapati bahagi  juga sama dengan darab dengan
juga sama dengan darab dengan 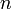
Pecahan bahagi nombor bulat
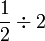
- Perhatikan
Perbandingan
Contoh
- a)
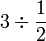
- b)
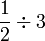
- c)
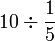
- d)
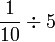
Gabungan
Kita sudah tahu
Jadi apakah yang berlaku bila
Contoh
Mari kita cuba gunakan cara ini dan tengok apakah maksud jawapannya
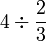
- Maksud
- a)
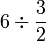
- b)
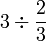
- c)
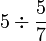
- a)
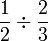
- b)
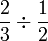
- c)
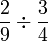
- d)
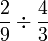
Perbandingan Tambah/Darab/Bahagi
Pecahan per Nombor / Nombor per Pecahan
- Apakah maksud
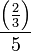 ?
?
- Apakah maksud
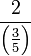 ?
?
Cuba
.png)
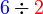 sebagai
sebagai
 kepada beberapa kumpulan yang setiap satu-nya ada
kepada beberapa kumpulan yang setiap satu-nya ada 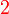
.png)
.png)
.png)
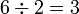
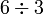
.png)
.png)
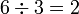
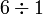
 dalam
dalam 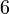 ?
?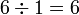
 dalam
dalam (2)s).png)
(2)s-label12).png)
(2)s-label12s).png)
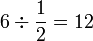
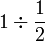
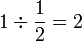
.png)
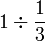
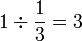
.png)
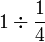
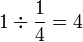
.png)
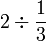
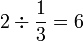
.png)
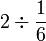
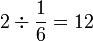
.png)
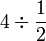
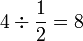
(2)s).png)
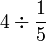
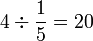
(5)s).png)
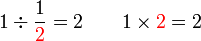
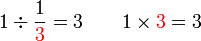
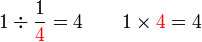
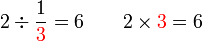
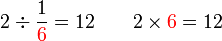
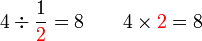
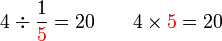
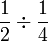
 dalam
dalam 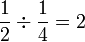
(2)-dotted-countfrac(1)(4)).png)
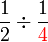 ?
?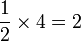 Ya
Ya
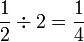
(2)-divide2red-dotted-to-frac(1)(4)-dotted).png)
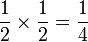 yang kita telah buat sebelum ini
yang kita telah buat sebelum ini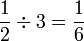
(2)-divide3red-dotted-to-frac(1)(6)-dotted).png)
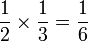 yang kita telah buat sebelum ini
yang kita telah buat sebelum ini
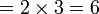
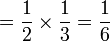

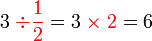
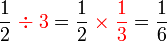
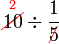 ?
?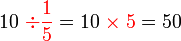
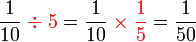
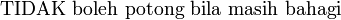
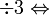
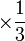
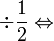
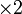
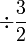
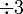 dan
dan 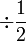
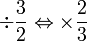
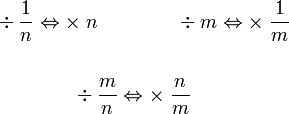
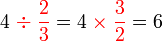
 dalam
dalam 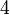 ?
?(3)-count-4-red).png)
(3)-count-4-red-2-blue).png)