Asas
Lorekkan pecahan yang berikut
.png)
|
.png)
|
.png)
|

|

|

|

Perbandingan Nilai
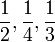
- Yang manakah yang mempunyai nilai yang paling besar?
- Yang manakah yang mempunyai nilai yang paling besar?
Lorekkan pecahan yang berikut
.png)
|
.png)
|
.png)
|

|

|

|

 menunjukkan
menunjukkan 
 menunjukkan
menunjukkan
- Kita dapat lihat bahawa
Lorekkan pecahan yang berikut
.png)
|
.png)
|
.png)
|

|

|

|

- Susun ikut nilai pecahan (besar ke kecil):
Penambahan/Penolakan Pecahan (dengan pembawah yang sama)
Penambahan/Penolakan Pecahan (dengan pembawah yang tidak sama)
Pecahan Setara
Yang manakah lebih besar?
Mari kita lihat bagaimana kita boleh mencari pecahan yang setara dengan
- Cuba kamu cari satu lagi pecahan yang setara dengan

Mempermudahkan Pecahan
.png)
|
.png)
|

|

|

Permudahkan pecahan-pecahan berikut
- a)
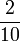
- b)
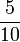
- c)
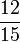
- d)
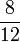
Ulangkaji Sifir
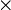
|
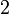
|
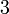
|
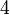
|
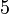
|
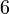
|
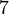
|
|
|
|
||||||||
|
||||||||
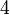
|
||||||||
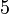
|
||||||||
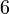
|
||||||||
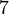
|
||||||||
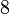
|
||||||||
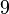
|
Tulis sebagai hasil-hasil darab dua nombor (kecuali 1, kalau tidak boleh biarkan)
Keboleh-bahagi-an dengan
Ada beberapa nombor yang senang kita semak samaada boleh dibahagi dengan atau tidak
Permudahkan pecahan-pecahan berikut JIKA boleh
Dua
- a)

- b)

- c)

- d)

- e)

- f)

- g)

- h)

- i)
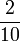
- j)
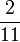
- k)
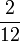
- l)
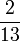
- m)
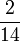
- n)
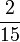
- o)
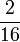
Tiga
- a)

- b)

- c)

- d)

- e)

- f)

- g)
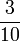
- h)
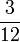
- i)
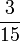
- j)
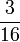
- k)
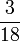
- l)
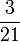
Empat, Lima, Enam
- a)

- b)

- c)
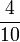
- d)
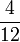
- e)
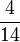
- f)
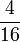
- g)
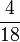
- h)
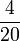
- i)
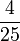
- j)
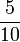
- k)
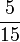
- l)
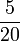
- m)
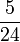
- n)
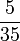
- o)
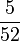
- p)

- q)

- r)
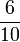
- s)
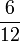
- t)
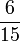
- u)
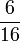
- v)
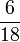
- w)
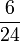
- x)
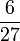
Lapan, Sembilan, Sepuluh, dsb
- a)
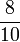
- b)
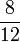
- c)
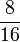
- d)
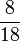
- e)
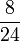
- f)
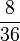
- g)
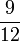
- h)
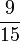
- i)
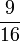
- j)
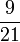
- k)
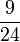
- l)
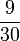
- m)
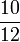
- n)
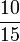
- o)
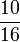
- p)
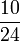
- q)
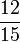
- r)
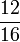
- s)
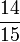
- t)
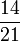
- u)
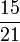
- v)
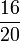
- w)
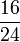
- x)
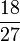
Penambahan/Penolakan Pecahan (Permudahkan jawapan)
- a)
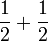
- b)
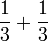
- c)
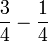
- d)
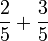
- e)
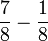
Penukaran Pembawah
- a)
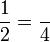
- b)
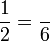
- c)
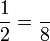
- d)
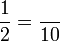
- e)
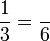
- f)
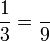
- g)
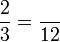
- h)
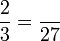
- i)
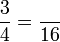
- j)
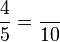
- k)
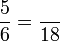
- l)
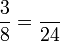
Penambahan/Penolakan dengan Pembawah Tidak Sama (besar boleh dibahagi kecil)
- a)
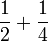
- b)
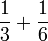
- c)
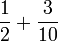
- d)
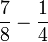
Penambahan/Penolakan dengan Pembawah Tidak Sama (tiada faktor sepunya)
Penambahan/Penolakan dengan Pembawah Tidak Sama (ada faktor sepunya)
- a)
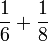
- b)
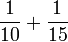
- c)
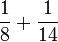
Kaedah lain mencari GSTK
- Kita dapat lihat pengiraan cara di atas agak sukar untuk nombor yang besar, jadi kita juga boleh menggunakan kaedah pembahagian berulang untuk mendapatkan GSTK dengan lebih cepat.
- Sebelum itu, adalah penting untuk mengetahui bila kita akan terus darab pembawah and bila kita akan cari yang lebih kecil dari itu
- Perhatikan contoh dari latihan di mana kita terus darab
- a)
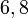
- b)

- c)
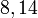
Penambahan/Penolakan Pecahan (Bercampur)
- a)
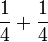
- b)
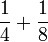
- c)
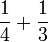
- d)
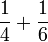
- e)

- f)
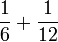
- g)
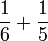
- h)
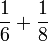
- i)
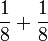
- j)
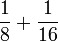
- k)
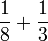
- l)
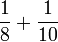
Dua
- a)
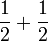
- b)
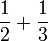
- c)
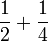
- d)
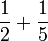
- e)
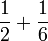
- f)
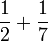
- g)
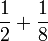
- h)
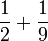
- i)
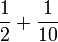
Tiga
- a)
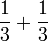
- b)
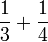
- c)
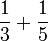
- d)
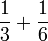
- e)
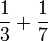
- f)
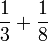
- g)
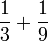
- h)
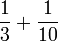
- i)
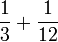
- j)
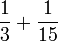
Empat
- a)
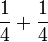
- b)
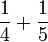
- c)
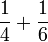
- d)
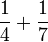
- e)
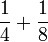
- f)
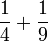
- g)
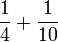
- h)
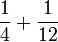
- i)
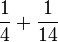
- j)
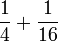
- k)
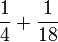
Lima
- a)
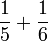
- b)
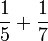
- c)
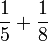
- d)
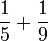
- e)
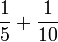
- f)
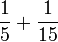
Enam
- a)
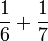
- b)
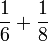
- c)
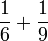
- d)
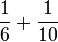
- e)
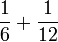
- f)
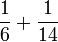
- g)
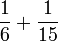
- h)
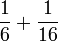
- i)
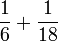
- j)
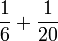
Tujuh, Lapan, Sembilan
- a)
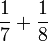
- b)
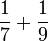
- c)
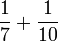
- d)
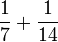
- e)
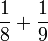
- f)
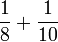
- g)
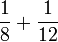
- h)
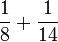
- i)
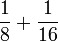
- j)
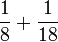
- k)
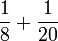
- l)
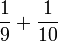
- m)
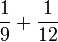
- n)
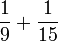
- o)
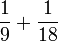
Sepuluh, dsb
- a)
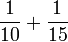
- b)
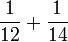
- c)
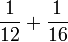
- d)
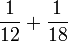
- e)
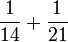
- f)
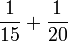
- g)
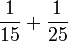
- h)
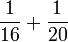
- i)
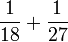
- j)
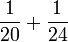
- k)
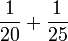
Bercampur
- a)
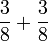
- b)
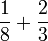
- c)
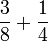
- d)
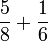
- e)
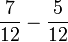
- f)
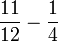
- g)
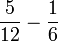
- h)
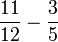
- i)
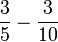
Kaedah Darab Silang
Kita lihat balik kes di mana kita menambah/menolak pecahan dengan pembawah yang tidak mempunyai faktor sepunya
- a)
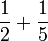
- b)
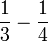
- c)
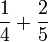
- d)
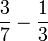
Yang manakah sesuai gunakan kaedah darab silang ?
Penambahan/Penolakan pecahan dengan nombor bulat
Nombor Bercampur
Apakah maksud 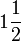 sebenarnya?
sebenarnya?
Jika kita faham sudah maksud nombor bercampur, kita juga boleh terus kira dengan
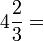
- atau terus
- a)
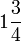
- b)
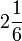
- c)
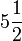
- d)
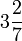
- e)
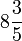
(2)).png)
(4)).png)
(4)-e-frac(1)(4)-e-frac(1)(2)).png)
(3)).png)
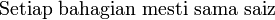
(2)).png/80px-Fracdiag(frac(1)(2)).png)
(4)).png/80px-Fracdiag(frac(1)(4)).png)
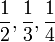
 menunjukkan
menunjukkan (4)-empty).png)
 menunjukkan
menunjukkan (4)).png)
 menunjukkan
menunjukkan (3)-empty).png)
(3)).png)
 menunjukkan
menunjukkan (5)-empty).png)
(4)frac(1)(4)frac(1)(6)frac(1)(6)frac(1)(6)-empty).png/80px-Fracdiag(frac(1)(4)frac(1)(4)frac(1)(6)frac(1)(6)frac(1)(6)-empty).png)
(8)frac(1)(8)frac(1)(4)frac(1)(4)frac(1)(4)-empty).png/80px-Fracdiag(frac(1)(8)frac(1)(8)frac(1)(4)frac(1)(4)frac(1)(4)-empty).png)
(5)).png)

(4)).png)
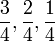
.png)
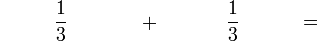
(3)-blue%2bfrac(1)(3)-red%3dcircle).png)
(3)-blue%2bfrac(1)(3)-red%3dfrac(1)(3)-blue-empty).png)
(3)-blue%2bfrac(1)(3)-red%3dfrac(1)(3)-blue-frac(1)(3)-red).png)

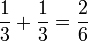 ?
?(3)-blue%2bfrac(1)(3)-red%3dfrac(1)(6)-blue-frac(1)(6)-red).png)
 Betul? Kenapa?
Betul? Kenapa?
(5)-empty%2bfrac(1)(5)-empty%3dcircle).png)
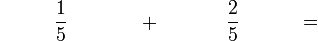
(5)%2bfrac(2)(5)%3dcircle).png)
(5)%2bfrac(2)(5)%3dfrac(3)(5)).png)

(5)-empty-frac(1)(5)-empty%3dcircle).png)

(5)-frac(2)(5)%3dcircle).png)
(5)-frac(2)(5)%3dfrac(1)(5)).png)


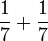
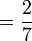
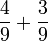
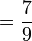
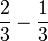
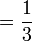
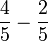
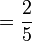
(2)%2bfrac(1)(4)%3dcircle).png)
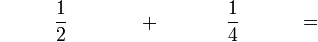
(2)-blue-%2bfrac(1)(4)-red-%3dfrac(1)(2)-blue-frac(1)(4)-red).png)
(2)-blue-%2bfrac(1)(4)-red-%3dfrac(1)(2)-blue-divide2-frac(1)(4)-red).png)

(2)-blue-divide2-%2bfrac(1)(4)-red-%3dfrac(1)(2)-blue-divide2-frac(1)(4)-red).png)
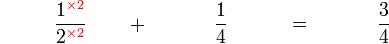
(8)%2bfrac(1)(4)%3dcircle).png)
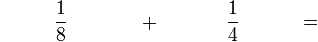
(8)-blue-%2bfrac(1)(4)-red-%3dfrac(1)(8)-blue-frac(1)(4)-red-).png)
(8)-blue-%2bfrac(1)(4)-red-%3dfrac(1)(8)-blue-frac(1)(4)-red-divide2).png)

(8)-blue-%2bfrac(1)(4)-red-divide2-%3dfrac(1)(8)-blue-frac(1)(4)-red-divide2).png)
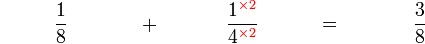

(3)-and-frac(2)(6)).png)

(3)-blue-and-frac(2)(6)-red-).png)
(3)-blue-and-frac(1)(3)-red-).png)
(3)%3dfrac(2)(6)).png)

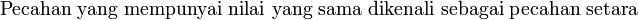


(2)-divide2).png)


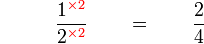
(2)-divide4).png)
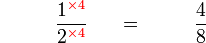
(2)-divide3).png)
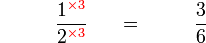

(8)).png)


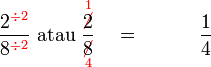
(6)).png)

(3)-1-3).png)
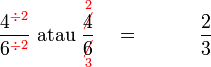
(9)).png)

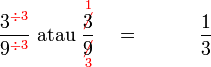

(2)).png)

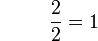
(3)).png)
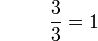
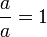
 boleh dibahagi dengan
boleh dibahagi dengan 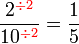 atau
atau 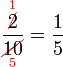
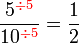 atau
atau 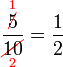
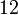 boleh bahagi
boleh bahagi 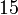 tidak boleh
tidak boleh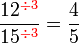 atau
atau 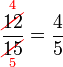
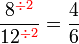 atau
atau 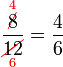
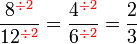 atau
atau 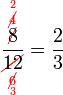
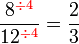 atau
atau 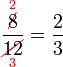

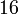

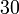
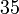
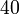
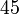
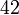
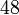
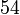
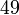
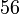
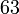
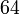
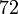
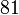
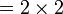
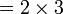
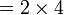
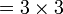
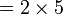
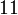
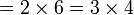
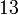
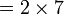
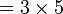
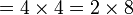
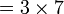
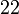
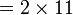
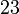
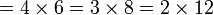
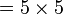
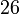
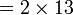
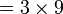
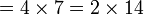
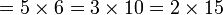
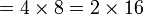
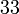
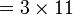
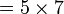
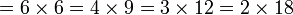
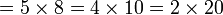
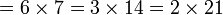
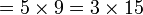
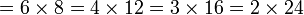
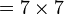
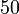
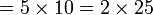
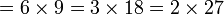
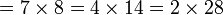
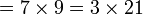
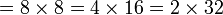
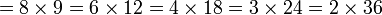
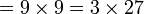
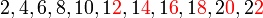
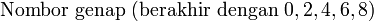
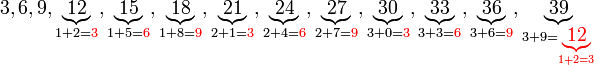
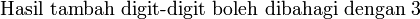
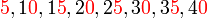
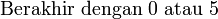
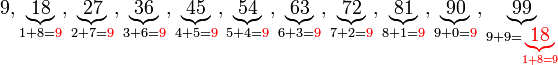
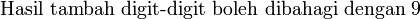

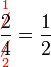 atau
atau 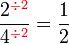
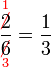 atau
atau 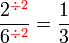
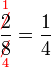 atau
atau 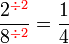
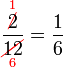 atau
atau 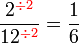
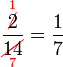 atau
atau 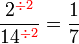
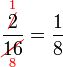 atau
atau 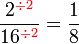
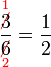 atau
atau 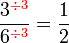
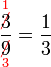 atau
atau 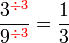
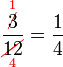 atau
atau 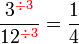
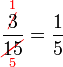 atau
atau 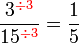
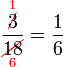 atau
atau 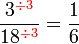
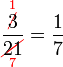 atau
atau 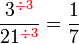
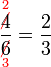 atau
atau 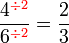
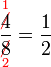 atau
atau 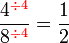
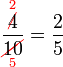 atau
atau 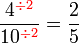
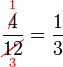 atau
atau 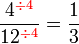
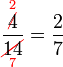 atau
atau 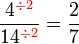
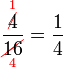 atau
atau 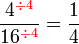
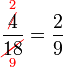 atau
atau 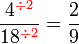
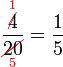 atau
atau 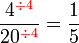
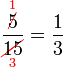 atau
atau 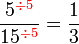
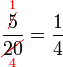 atau
atau 
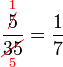 atau
atau 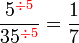
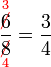 atau
atau 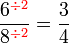
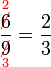 atau
atau 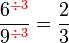
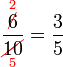 atau
atau 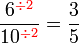
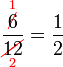 atau
atau 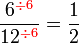
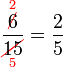 atau
atau 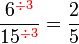
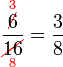 atau
atau 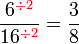
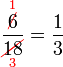 atau
atau 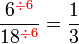
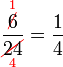 atau
atau 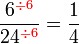
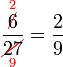 atau
atau 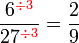
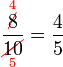 atau
atau 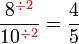
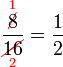 atau
atau 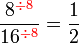
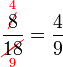 atau
atau 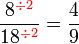
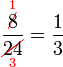 atau
atau 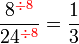
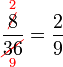 atau
atau 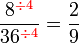
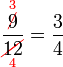 atau
atau 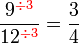
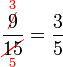 atau
atau 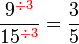
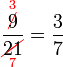 atau
atau 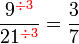
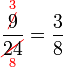 atau
atau 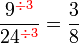
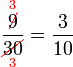 atau
atau 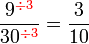
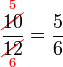 atau
atau 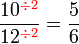
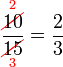 atau
atau 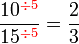
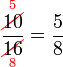 atau
atau 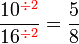
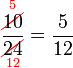 atau
atau 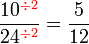
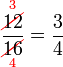 atau
atau 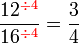
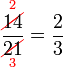 atau
atau 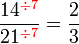
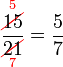 atau
atau 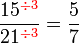
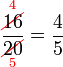 atau
atau 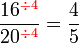
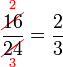 atau
atau 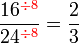
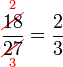 atau
atau 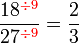
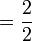 Siap?
Siap?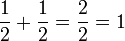
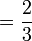 Siap?
Siap?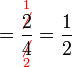
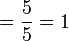
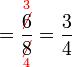
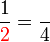 ke
ke 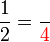
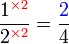
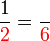
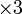 atas dan bawah
atas dan bawah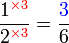
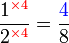
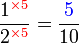
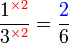
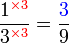
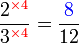
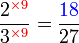
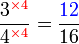
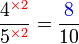
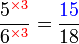
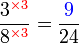
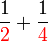
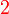 boleh ditukar ke
boleh ditukar ke 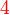 , jadi pembawah jawapan ialah
, jadi pembawah jawapan ialah 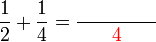
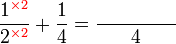
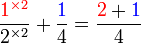
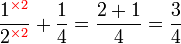
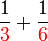
 boleh ditukar ke
boleh ditukar ke  , jadi pembawah jawapan ialah
, jadi pembawah jawapan ialah 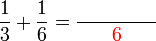
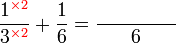
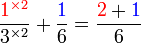
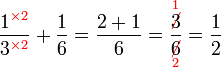
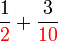
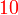 , jadi pembawah jawapan ialah
, jadi pembawah jawapan ialah 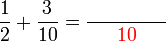
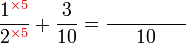
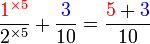
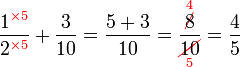
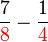
 , jadi pembawah jawapan ialah
, jadi pembawah jawapan ialah 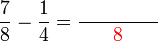
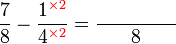
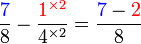
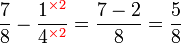

(3)%2bfrac(1)(2)%3dcircle).png)
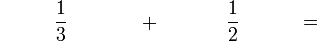
(3)-blue-%2bfrac(1)(2)-red-%3dfrac(1)(3)-blue).png)
(3)-blue-%2bfrac(1)(2)-red-%3dfrac(1)(3)-blue-frac(1)(2)-red).png)
(3)-blue-%2bfrac(1)(2)-red-%3dfrac(1)(3)-blue-frac(1)(2)-red-divide2).png)
(3)-blue-%2bfrac(1)(2)-red-%3dfrac(1)(3)-blue-frac(1)(2)-red-divide-to-frac(2)(3)).png)
(3)-blue-%2bfrac(1)(2)-red-%3dfrac(1)(3)-blue-divide2-frac(1)(2)-red-divide3).png)

(3)-blue-divide2-%2bfrac(1)(2)-red-divide3-%3dfrac(1)(3)-blue-divide2-frac(1)(2)-red-divide3).png)
 , setiap bahagian dibahagi
, setiap bahagian dibahagi  , setiap bahagian dibahagi
, setiap bahagian dibahagi 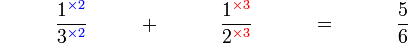
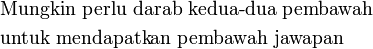
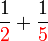
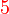
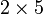
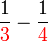
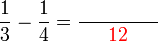
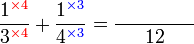
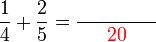
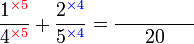
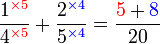
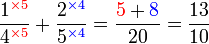
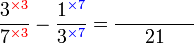
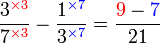
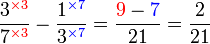
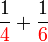
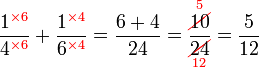
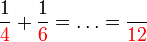
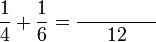
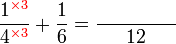
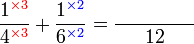
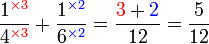

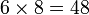 ataupun ada yang lebih kecil lagi?
ataupun ada yang lebih kecil lagi?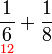
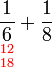 Tidak boleh
Tidak boleh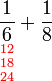 OK!
OK!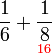
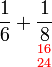
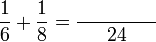
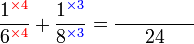
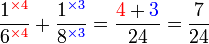
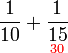 atau
atau 
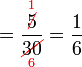
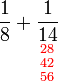
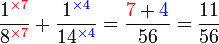
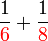
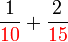
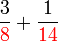
.png)
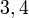 , sebenarnya kita boleh terus kira GSTK sebagai
, sebenarnya kita boleh terus kira GSTK sebagai-red(2%2c3%2c4).png)
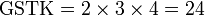
.png)
.png)
-red(5%2c2%2c3).png)
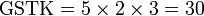
.png)
-red(2%2c4%2c7).png)
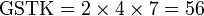
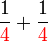
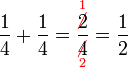
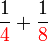
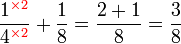
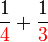
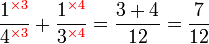
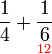 atau
atau 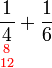
.png)
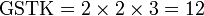
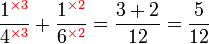
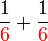
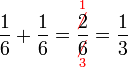
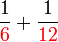
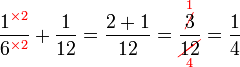
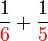
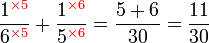
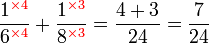
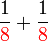
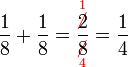
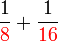
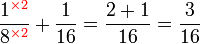
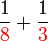
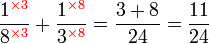
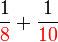
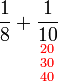
.png)
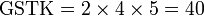
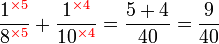

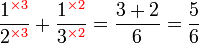
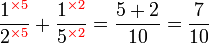
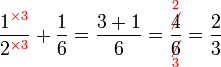
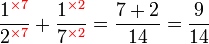
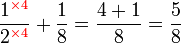
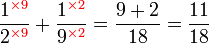
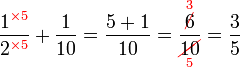
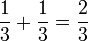
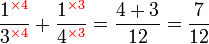
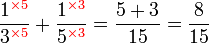
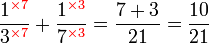
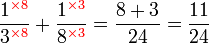
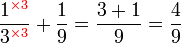
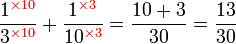
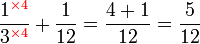
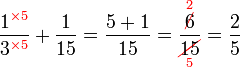
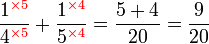
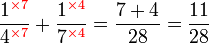
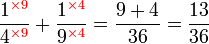
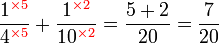
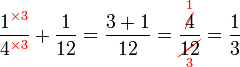
.png)
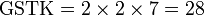
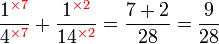
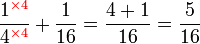
.png)
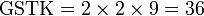
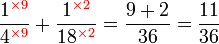
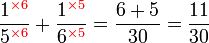
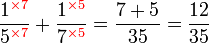
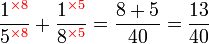
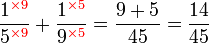
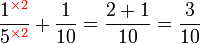
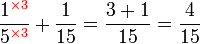
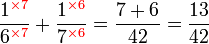

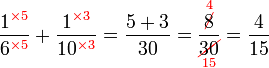
.png)
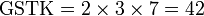
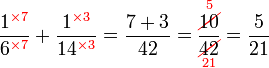
.png)
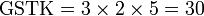
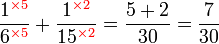
.png)
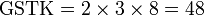
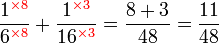
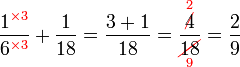
.png)
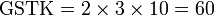
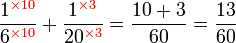
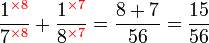
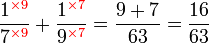
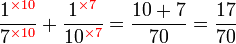
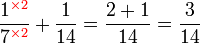
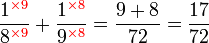
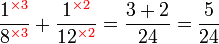
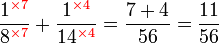
.png)
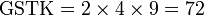
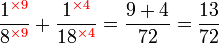
.png)
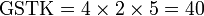
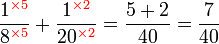
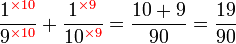
.png)
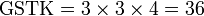
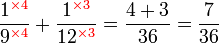
.png)
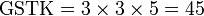
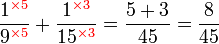
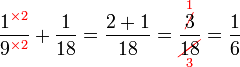
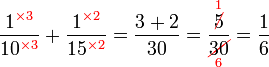
.png)
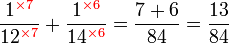
.png)
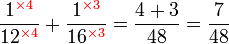
.png)
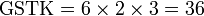
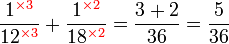
.png)
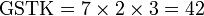
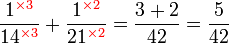
.png)
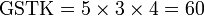
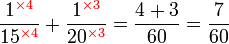
.png)
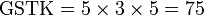
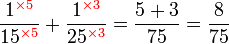
.png)
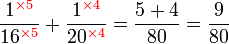
.png)
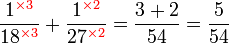
.png)
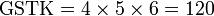
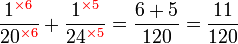
.png)
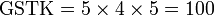
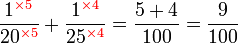
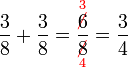
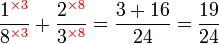
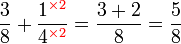
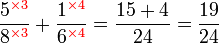
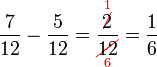
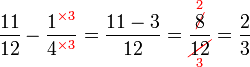
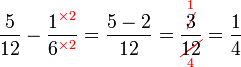
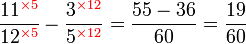
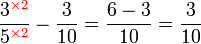
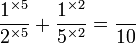
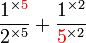
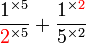
(2)%2bfrac(1)(5)).png)
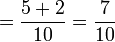
(3)-frac(1)(4)).png)
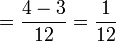
(4)%2bfrac(2)(5)).png)
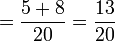
(7)-frac(1)(3)).png)
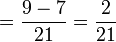

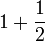 ? (ditulis dalam pecahan tidak wajar)
? (ditulis dalam pecahan tidak wajar)
.png)
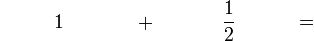
(2)).png)
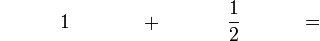
(2)).png)
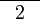
(2)-countparts).png)
 2 bahagian
2 bahagian  1 bahagian
1 bahagian 
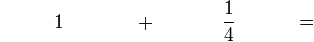
(4)).png)
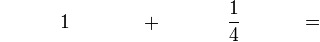
(4)).png)
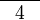
(4)-countparts).png)
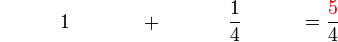
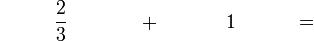
(3)%2b1).png)
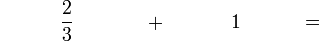
(3)%2b1-divide3).png)
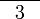
(3)%2b1-divide3-countparts).png)
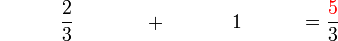
(5)).png)

(5)).png)
(5)-countparts).png)
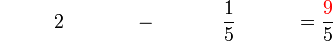
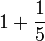

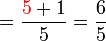
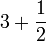
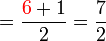
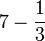
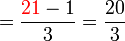
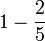
(5)).png)
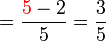
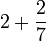
(7)).png)
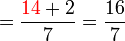
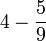
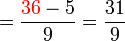
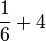
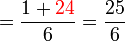
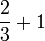
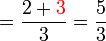
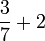
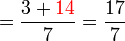
(c)frac(a)(b)%2bca-frac(b)(c)frac(a)(b)-c).png)
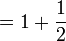
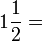
(2)).png)
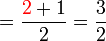
(3)).png)
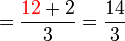
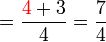
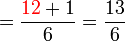
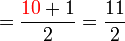
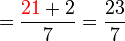
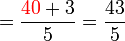
(c)%3dfrac(atimesc%2bb)(c)).png)