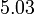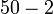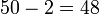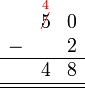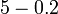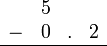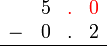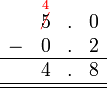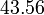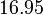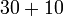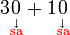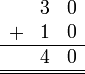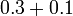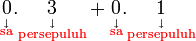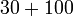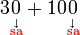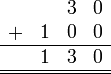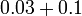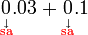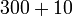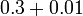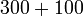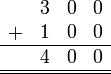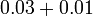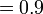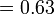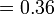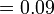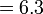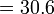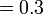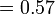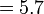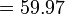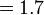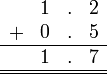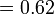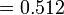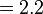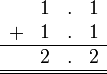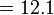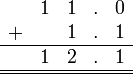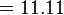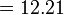Maksud Perpuluhan
Guna Tatatanda Pecahan
- Sekarang, bayangkan kita ambil bahagian yang panjangnya 1, dan diperbesarkan
Tatatanda perpuluhan
- Kita sudah belajar nilai tempat yang biasa seperti
-
- Jadi
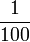

Guna Tatatanda Perpuluhan
- Sekarang kita guna tatatanda perpuluhan
Tulis sebagai perpuluhan
Tulis sebagai pecahan
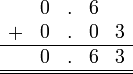
Penambahan/Penolakan
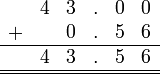
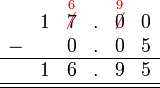
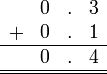
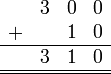
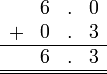
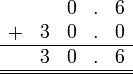
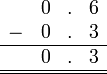
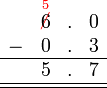
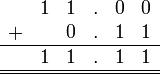
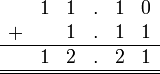
Sebelum kita tengok penambahan/penolakan nombor perpuluhan, kita ulangkaji balik penambahan biasa.
Cuba Sendiri
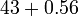
- Jwp :
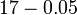
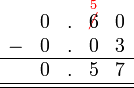
- Jwp :
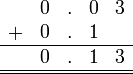
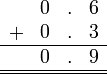
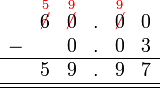
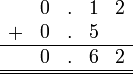
Perpuluhan dengan perpuluhan
Latihan 1
- a)

- b)
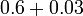
- c)
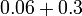
- d)
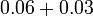
- e)
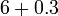
- f)
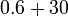
- g)
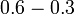
- h)
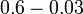
- i)
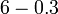
- j)
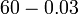
- k)
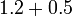
- l)
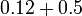
- m)
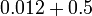
- n)
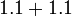
- o)
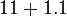
- p)
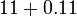
- q)
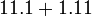
.png/800px-Ruler(100-10-1).png)
.png/800px-Ruler(100-10-1%2cred-10).png)
.png/800px-Ruler(100-10-1%2cred-10%2clabel10s).png)
.png/800px-Ruler(100-10-1%2cred-1).png)
.png/800px-Ruler(100-10-1%2cred-1%2clabel1s).png)
(10)-frac(1)(100)all).png/800px-Ruler(1-frac(1)(10)-frac(1)(100)all).png)
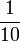
(10)-frac(1)(100)all%2cred-frac(1)(10)%2clabelfrac(1)(10)s).png/800px-Ruler(1-frac(1)(10)-frac(1)(100)all%2cred-frac(1)(10)%2clabelfrac(1)(10)s).png)
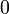 hingga
hingga (10)zoom).png/400px-Ruler(0-frac(1)(10)zoom).png)
(10)-frac(1)(100)all%2clabelfrac(1)(10)s%2ccount10).png/800px-Ruler(1-frac(1)(10)-frac(1)(100)all%2clabelfrac(1)(10)s%2ccount10).png)
(10)zoom%2clabelfrac(1)(100)).png/400px-Ruler(0-frac(1)(10)zoom%2clabelfrac(1)(100)).png)
 dengan
dengan  , kita mendapat bahagian-bahagian
, kita mendapat bahagian-bahagian 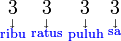
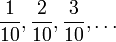 )
) 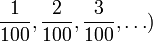 .
.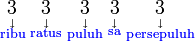



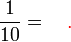
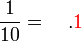
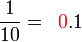
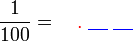
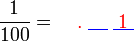




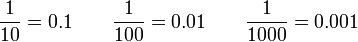
.png/800px-Ruler(1-0.1-0.01).png)
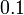
.png/800px-Ruler(1-0.1-0.01%2clabel0.1s).png)
.png/400px-Ruler(0-0.1zoom).png)
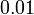
.png/400px-Ruler(0-0.1zoom%2clabel0.001s).png)
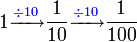
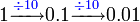
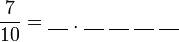
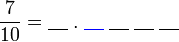
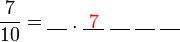
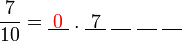
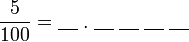
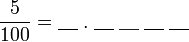
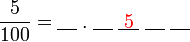
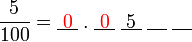
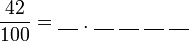
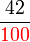 , nilai tempat adalah
, nilai tempat adalah 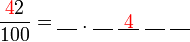
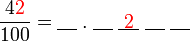 ?
?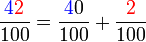 jadi sememangnya
jadi sememangnya 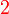 yang di tempat perseratus
yang di tempat perseratus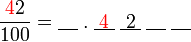
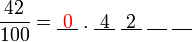
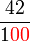 TIDAK bermaksud akan ada dua kosong
TIDAK bermaksud akan ada dua kosong
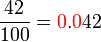 sudah tentu adalah SALAH.
sudah tentu adalah SALAH.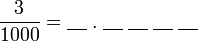
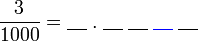
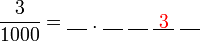
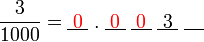
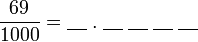
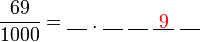
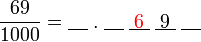
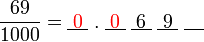
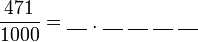
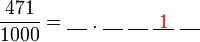
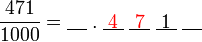
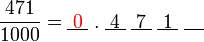
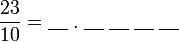
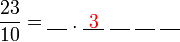
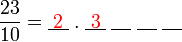
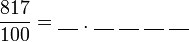

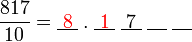
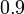
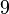 ?
?
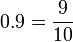
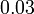
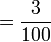
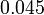
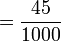
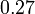
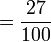
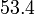
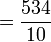
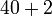
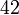
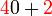 bukan
bukan  ?
?
 tidak mempunyai nilai dan tidak mempengaruhi jawapan?
tidak mempunyai nilai dan tidak mempengaruhi jawapan?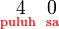
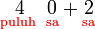

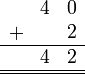
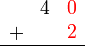
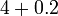
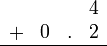
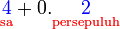
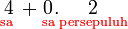

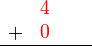
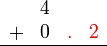
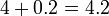
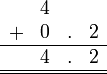
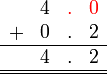
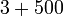
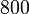 atau
atau 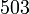 ?
?
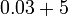
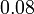 atau
atau 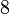 ?
?