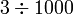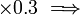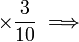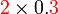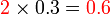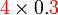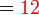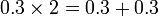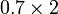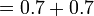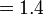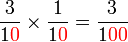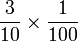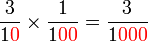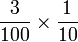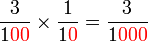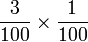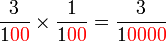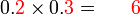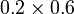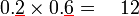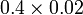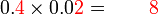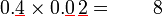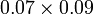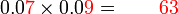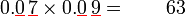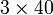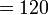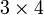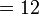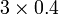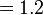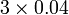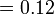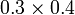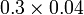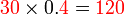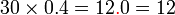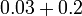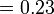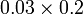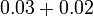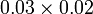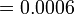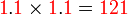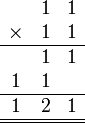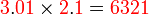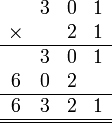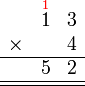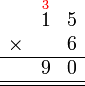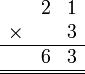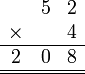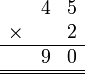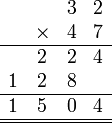Perbandingan Nilai
-
 lebih kecil berbanding
lebih kecil berbanding 
-
 lebih kecil berbanding
lebih kecil berbanding 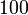
-
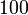 lebih besar berbanding
lebih besar berbanding 
-
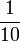 lebih kecil berbanding
lebih kecil berbanding 
-
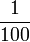 lebih kecil berbanding
lebih kecil berbanding 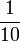
-
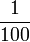 lebih besar berbanding
lebih besar berbanding 
-
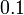 lebih kecil berbanding
lebih kecil berbanding 
-
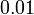 lebih kecil berbanding
lebih kecil berbanding 
-
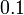 lebih besar berbanding
lebih besar berbanding 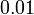
-
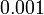 lebih kecil berbanding
lebih kecil berbanding 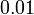
Isikan tempat kosong

- Bagaimanakah untuk menukarkan
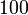 kepada
kepada  ?
? - Dengan bahagi 10
- Bagaimanakah untuk menukarkan

- Bagaimanakah pula untuk menukarkan
 kepada
kepada 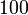 ?
? - Dengan mendarab 10
- Bagaimanakah pula untuk menukarkan
Darab 0.1
-
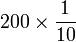
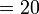
- Perhatikan bahawa
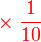 adalah sama dengan
adalah sama dengan 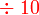
- Perhatikan bahawa
-
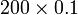
- Apakah pula nilai
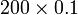 ?
? - Nilai
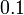 sebenarnya sama dengan
sebenarnya sama dengan 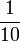
- Jadi
 sebenarnya sama dengan
sebenarnya sama dengan 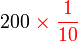 , yang sama dengan
, yang sama dengan 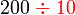
- Jadi
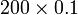
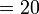
- Apakah pula nilai
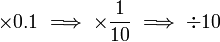
Contoh
- Analisis
- Perhatikan apa yang berlaku kepada nilai selepas didarab dengan
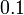
-
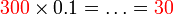
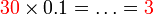
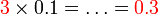
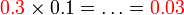
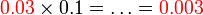
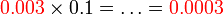
- Di mana semua nilai akan menjadi 10 kali ganda lebih kecil selepas darab
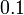
- Perhatikan apa yang berlaku kepada nilai selepas didarab dengan
- Melihat nombor perpuluhan
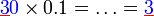
- Di manakah titik perpuluhan pada asalnya dan pada akhirnya?
-

Bandingkan
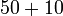
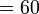
- Puluh tambah puluh, jawapan masih puluh juga (kecuali dalam kes 60 +70 begitu)
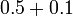
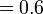
- Persepuluh tambah persepuluh, jawapan masih persepuluh
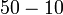
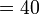
- Puluh tolak puluh, jawapan masih puluh juga (kecuali dalam kes 65- 60 begitu)
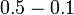
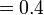
- Persepuluh tolak persepuluh, jawapan masih persepuluh juga
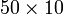
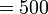
- Puluh darab puluh, jawapan menjadi ratus
-
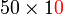 adalah penting, menentukan nilai tempat
adalah penting, menentukan nilai tempat - Nilai tempat akan berubah selepas darab

-
- Puluh darab puluh, jawapan menjadi ratus
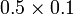
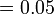
- Persepuluh darab persepuluh, menjadi perseratus
-
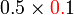 adalah penting, menentukan nilai tempat
adalah penting, menentukan nilai tempat - Nilai tempat akan berubah selepas darab
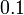
-
- Persepuluh darab persepuluh, menjadi perseratus
Darab 0.01, 0.001
-
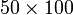
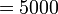
- Menjadi 100 kali lebih besar
-
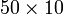
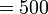
- Menjadi 10 kali lebih besar
-
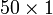
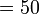
- Nilai tidak berubah
-
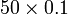
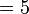
- Menjadi 10 kali lebih kecil
- Titik perpuluhan bergerak ke kiri satu langkah
-
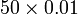
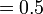
- Menjadi 100 kali lebih kecil
- Ini kerana
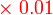 bersamaan dengan
bersamaan dengan 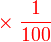 bersamaan dengan
bersamaan dengan 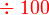
- Ini kerana
- Menjadi 100 kali lebih kecil
- Nilai tempat akan berubah dari puluh ke persepuluh (puluh ke sa ke persepuluh)
- Titik perpuluhan
-
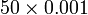
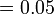
- Menjadi 1000 kali lebih kecil
- Ini kerana
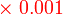 bersamaan dengan
bersamaan dengan 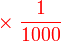 bersamaan dengan
bersamaan dengan 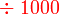
- Ini kerana
- Menjadi 1000 kali lebih kecil
- Nilai tempat akan berubah dari puluh ke perseratus (puluh ke sa ke persepuluh ke perseratus)
- Titik perpuluhan

Darab 10,100,1000
-
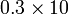
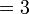
- Perhatikan bahawa nilai telah menjadi lebih besar sepuluh kali
- Nilai tempat
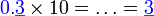
- Berubah dari persepuluh ke sa
- Sebelum ini, nilai menjadi lebih kecil, titik perpuluhan bergerak ke kiri
- Di sini, nilai menjadi lebih besar

Bahagi 10,100,1000
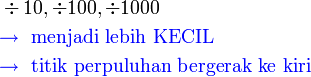
Darab perpuluhan
Apakah maksudnya untuk mendarab perpuluhan seperti 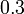 ?
?
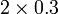
- Yang perlu dibuat adalah
- darab
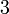
- dan bahagi

- darab
- Yang perlu dibuat adalah
- darab
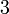

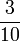 adalah kurang dari
adalah kurang dari 
- selepas

- nilai
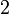 akan menjadi lebih kecil
akan menjadi lebih kecil
- nilai
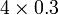
- Yang perlu dibuat adalah
- darab
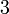
- bahagi

- darab
- Yang perlu dibuat adalah
- darab
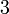

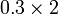
- Apakah pula maksud
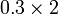 ? Ada dua
? Ada dua 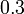 ditambah
ditambah -
- Apakah pula maksud
- Analisis
- Tengok bilangan tempat perpuluhan
-
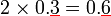
-
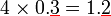
-
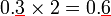
-
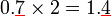
- Semua soalan mempunyai 1 tempat perpuluhan
- Semua jawapan mempunyai 1 tempat perpuluhan
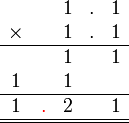
Darab perpuluhan dengan perpuluhan
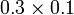
- Kita tahu sudah jawapannya
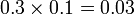
- (gerak titik perpuluhan yang asal ke kiri satu langkah)
- Jika kita banding tempat perpuluhan di soalan dan di jawapan
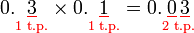
- Bilangan tempat perpuluhan pada jawapan (2) juga sama dengan jumlah (1+1) pada soalan.
- Ini adalah kerana pada asalnya mempunyai 1 tempat perpuluhan (persepuluh), kemudian mendarab yang mempunyai 1 tempat perpuluhan (persepuluh), akan menjadi perseratus (2 tempat perpuluhan).
- Kita tahu sudah jawapannya
- Jika soalan sama dilihat sebagai pecahan
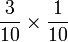
-
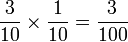
- Persepuluh darab persepuluh akan jadi perseratus
- Seakan-akan juga
-
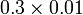
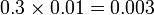
- (gerak titik perpuluhan yang asal ke kiri dua langkah)
-
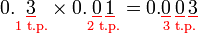
- Bilangan tempat perpuluhan pada jawapan (3) juga sama dengan jumlah (1+2) pada soalan.
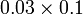
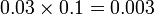
- (gerak titik perpuluhan yang asal ke kiri satu langkah)
-
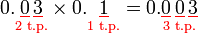
- Bilangan tempat perpuluhan pada jawapan (3) juga sama dengan jumlah (2+1) pada soalan.
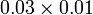
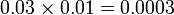
- (gerak titik perpuluhan yang asal ke kiri dua langkah)
-
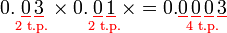
- Bilangan tempat perpuluhan pada jawapan (4) juga sama dengan jumlah (2+2) pada soalan.

Contoh
-
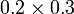
- Kita tahu jawapannya mempunyai tempat perpuluhan yang sama dengan jumlah tempat perpuluhan yang didarab
- Tetapi
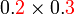 masih perlu didarab
masih perlu didarab - Jadi langkah pertama adalah
- Darab dulu nilainya TANPA melihat tempat perpuluhan
-
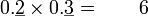
- jumlahnya 2 t.p.
- Perhatikan oleh kerana

- kita sedang mendarab suatu nilai yang lebih kecil dari

- Nilai
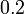 telah menjadi
telah menjadi
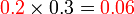
- lebih kecil selepas didarab
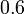 adalah kurang dari 1 dan besar sedikit dari
adalah kurang dari 1 dan besar sedikit dari 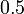 ( yang sama nilainya dengan
( yang sama nilainya dengan  )
)- Jadi selepas darab dengan
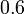

- Nilai menjadi lebih kurang separuh dari asalnya
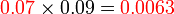
- Nilai menjadi lebih kurang 10 kali ganda lebih kecil, dan ini adalah kerana
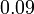 adalah hampir sama dengan
adalah hampir sama dengan 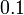
- Nilai menjadi lebih kurang 10 kali ganda lebih kecil, dan ini adalah kerana
Contoh
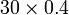
- Kita boleh darab dulu
- Kemudian letak titik perpuluhan
- Apapun cara, cuba lihat jawapan akhir samaada logik ataupun tidak
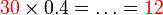
- 30 menjadi sedikit lebih kecil daripada separuh nilai asalnya selepas mendarab 0.4
- Kita boleh darab dulu
Bandingkan
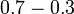
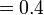
- Tempat perpuluhan tidak berubah bila tambah/tolak
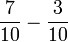
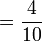
- Pembawah tidak berubah bila tambah/tolak pecahan dengan pembawah sama
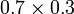
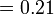
- Jumlahkan tempat perpuluhan bila darab
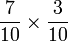
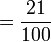
- Darabkan pembawah bila darab pecahan
Bandingkan
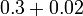
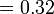
- Tambah/tolak ikut tempat perpuluhan
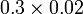
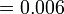
- Tempat perpuluhan perlu ditambah bila darab
Pendaraban Bentuk Lazim
-
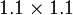 akan memberikan nilai yang hampir dengan ?
akan memberikan nilai yang hampir dengan ?
- A)

- B)

- C)
- D)
- A)
-
- Nilai
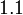 adalah hampir dengan
adalah hampir dengan  ataupun
ataupun  ?
?
-
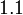 adalah hampir sama dengan
adalah hampir sama dengan 
-
- Nilai
- Jadi nilai
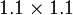 akan hampir dengan
akan hampir dengan 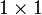 , iaitu
, iaitu 
- Apapun cara pengiraan yang digunakan, adalah penting untuk menyemak jawapan samaada logik ataupun tidak
- Kita boleh membuat pengiraan secara dua langkah seperti cara tadi, iaitu
- mendarab tanpa melihat tempat perpuluhan
- menjumlahkan tempat perpuluhan
- Kira dulu (tidak perlu letak tempat perpuluhan dalam bentuk lazim)
- Pasitkan jawapan adalah logik
-
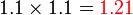
- adalah lebih besar sedikit daripada
-
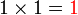
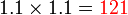 seratus lebih
seratus lebih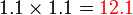 dua belas lebih
dua belas lebih- Yang sememangnya tidak logik
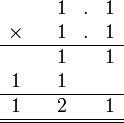
-
- Paling baik jangan
- Adalah mudah untuk membuat kesilapan seperti
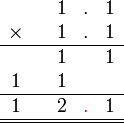 kerana mudah terkeliru dengan
kerana mudah terkeliru dengan 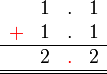
-
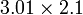 akan memberikan nilai yang hampir dengan ?
akan memberikan nilai yang hampir dengan ?
- A)
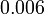
- B)
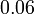
- C)
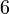
- D)
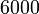
- C)
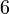
- A)
- Patutka kita menyusun
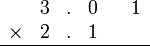 atau
atau 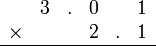
-
- Kita perlu lihat balik pendaraban lazim nombor biasa
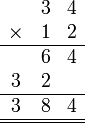
- Apakah sebabnya kita susun sebegini?
-
- Pendaraban dengan sa

- ditulis mula ditempat asal
- Pendaraban dengan puluh

- di"gerakkan" ke kiri satu langkah
- Pendaraban dengan sa
- Jadi sepatutnya disusun
- Supaya
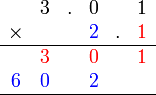
- TETAPI sebenarnya lebih baik JANGAN tulis tempat perpuluhan untuk pendaraban secara lazim
- Darab tanpa melihat tempat perpuluhan
-
-
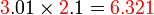
- Lebih besar sedikit dari 6 (hasil darab 2 dengan 3)
Latihan 2
- a)
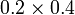
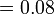
- b)
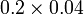
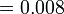
- c)
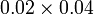
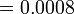
- d)

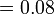
- e)
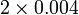
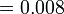
- f)
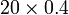
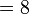
- g)
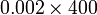
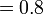
- h)
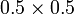
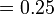
- i)
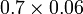
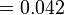
- j)
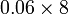
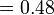
- k)
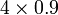
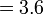
- l)
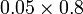
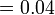
- m)
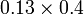
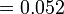
-
- n)
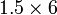
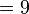
-
- o)
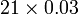
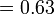
-
- p)
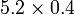
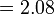
-
- q)
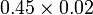
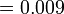
-
- r)
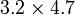
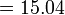
-
- s)
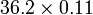
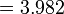
-
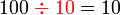
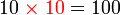

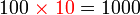
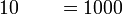


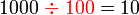
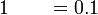


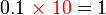
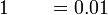
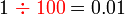

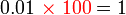

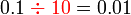

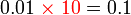
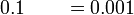


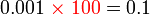
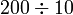
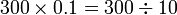
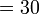
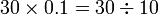
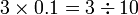
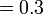
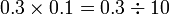
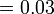
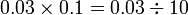
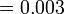
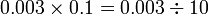
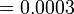
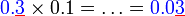
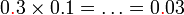
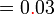
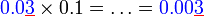
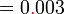
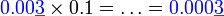
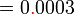
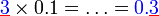
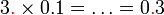
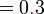
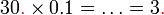
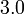 sebagai jawapan kerana
sebagai jawapan kerana 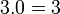
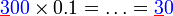
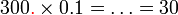
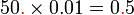
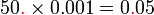
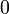 perlu ditambahkan di mana perlu
perlu ditambahkan di mana perlu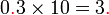
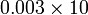
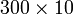
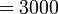
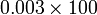
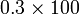
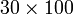
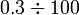
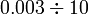
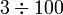
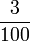 kepada perpuluhan
kepada perpuluhan