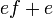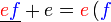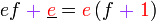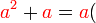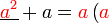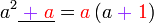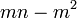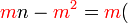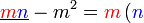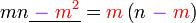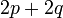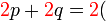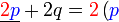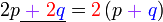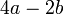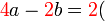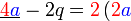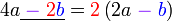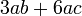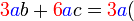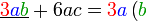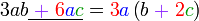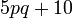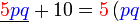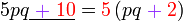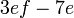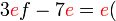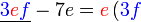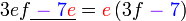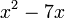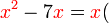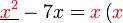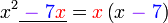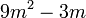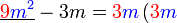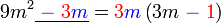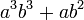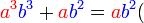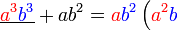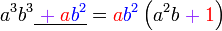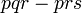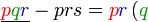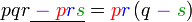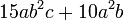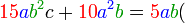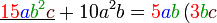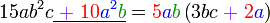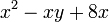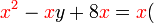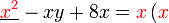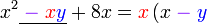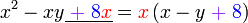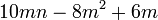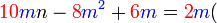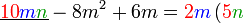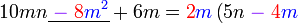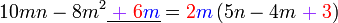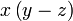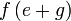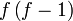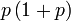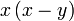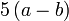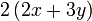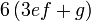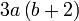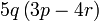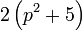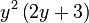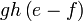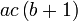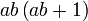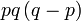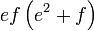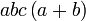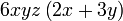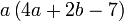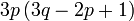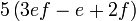Pemfaktoran sebagai songsang pengembangan
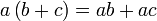 dipanggil
dipanggil
- Apakah yang sebenarnya dilakukan dalam proses pemfaktoran ?
Menentukan FSTB
Kita kaji dulu pelbagai kes pengembangan untuk melihat bagaimana kita hendak mengenalpasti faktor yang perlu "dikeluarkan".
|
Yang difaktorkan | ||
|---|---|---|
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
| ||
Contoh
|
FSTB | ||
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Menentukan faktor yang tertinggal
Isikan tempat kosong
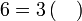
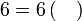
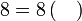
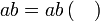
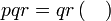

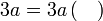
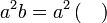
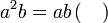
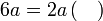
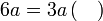
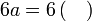
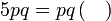
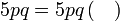
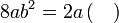
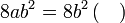
Pemfaktoran
Latihan 9
Faktorkan dengan lengkap
- a)
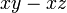
- Jwp :
- b)
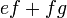
- Jwp :
- c)
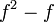
- Jwp :
- d)
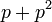
- Jwp :
- e)
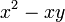
- Jwp :
- f)
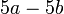
- Jwp :
- g)
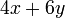
- Jwp :
- h)
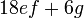
- Jwp :
- i)
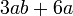
- Jwp :
- j)
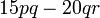
- Jwp :
- k)
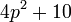
- Jwp :
- l)
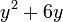
- Jwp :
- m)
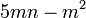
- Jwp :
- n)
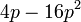
- Jwp :
- o)
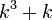
- Jwp :
- p)

- Jwp :
- q)
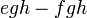
- Jwp :
- r)
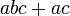
- Jwp :
- s)
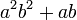
- Jwp :
- t)
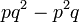
- Jwp :
- u)
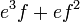
- Jwp :
- v)
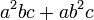
- Jwp :
- w)
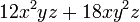
- Jwp :
- x)
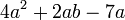
- Jwp :
- y)
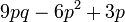
- Jwp :
- z)
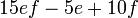
- Jwp :
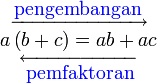
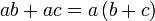
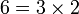 , yang dikatakan sebagai faktor adalah
, yang dikatakan sebagai faktor adalah 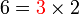
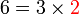
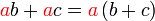
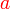 merupakan
merupakan
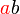
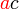

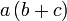
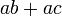

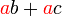
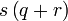
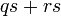

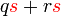
 dapat "dilihat" di kedua-dua sebutan
dapat "dilihat" di kedua-dua sebutan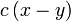
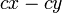

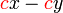
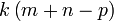
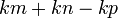
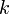
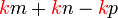
 dapat "dilihat" di ketiga-tiga sebutan
dapat "dilihat" di ketiga-tiga sebutan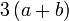
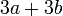
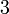
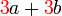
 yang difaktorkan
yang difaktorkan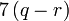
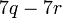
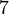
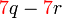
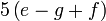
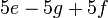
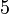
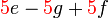
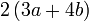
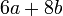
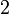
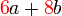
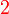 yang difaktorkan
yang difaktorkan
 dan
dan  kedua-duanya boleh dibahagi dengan
kedua-duanya boleh dibahagi dengan 
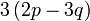
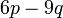
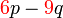

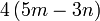
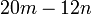
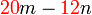
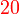 dan
dan 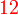 kedua-duanya boleh dibahagi dengan
kedua-duanya boleh dibahagi dengan 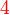
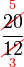
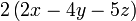
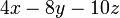
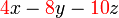
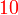 ketiga-tiganya boleh dibahagi dengan
ketiga-tiganya boleh dibahagi dengan 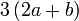
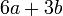
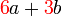
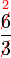
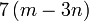
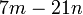
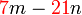
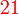 boleh dibahagi dengan
boleh dibahagi dengan 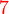
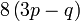
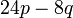
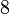
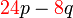
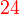 boleh dibahagi dengan
boleh dibahagi dengan 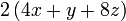
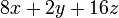
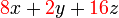
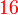 boleh dibahagi dengan
boleh dibahagi dengan 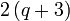
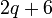
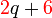
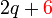
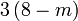
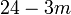
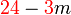
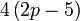
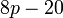
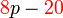
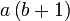
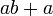
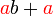
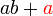
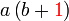
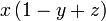
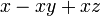

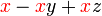
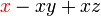
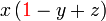
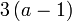
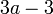
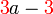

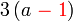
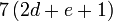
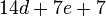
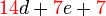
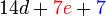
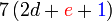
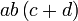
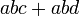
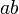
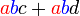
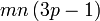
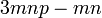
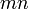
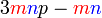
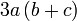
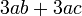
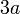
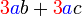
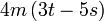
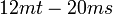
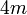
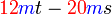
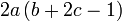
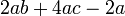
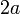
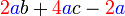
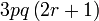
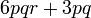
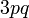
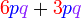
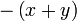
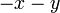

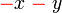

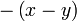
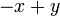
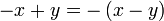
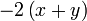
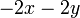
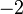
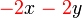
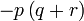
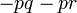
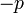
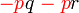
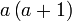
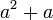
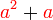
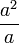
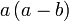
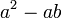
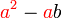
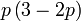
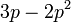

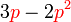
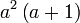
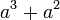
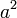
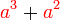
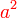 difaktorkan
difaktorkan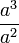
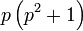
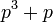
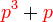
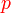 sahaja difaktorkan
sahaja difaktorkan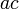
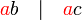
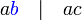
 bukan faktor sepunya
bukan faktor sepunya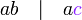
 bukan faktor sepunya
bukan faktor sepunya 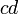
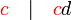
 ialah faktor sepunya
ialah faktor sepunya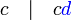
 bukan faktor sepunya
bukan faktor sepunya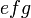
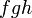
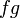
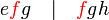
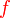 ialah faktor sepunya
ialah faktor sepunya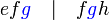
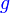 ialah faktor sepunya juga
ialah faktor sepunya juga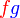
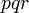
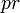
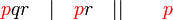
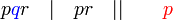
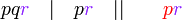
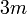
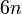
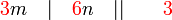
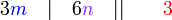
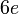
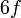
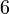
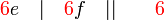
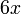
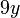
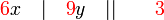
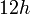
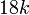
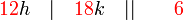
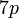
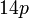
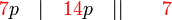
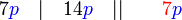
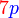
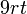
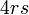


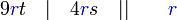
 sahaja
sahaja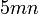
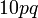
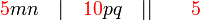
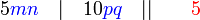
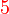 sahaja
sahaja
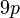
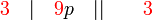
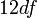
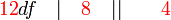
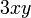
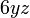
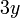
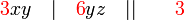
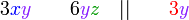
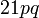
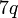
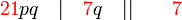
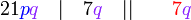

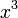
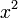
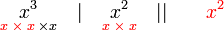
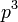
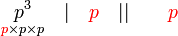
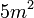
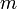
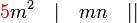
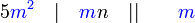
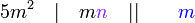
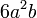
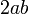
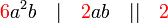
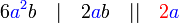
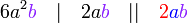
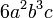
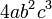
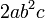
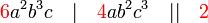
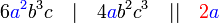
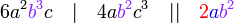
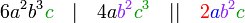

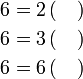
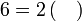
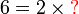
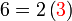
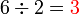
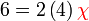
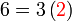
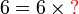 atau
atau 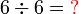
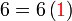
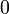 atau tidak tulis apa-apa
atau tidak tulis apa-apa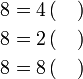
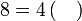
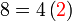
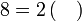
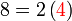
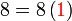
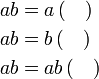
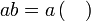
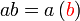
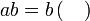
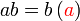
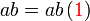

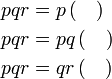
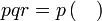
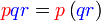
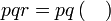
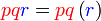
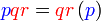
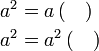
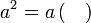
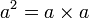
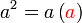
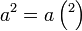
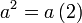
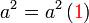
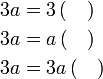
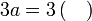
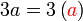
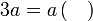
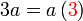
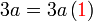
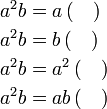
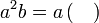
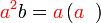
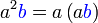
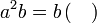
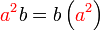
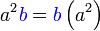
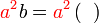
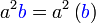
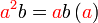
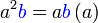
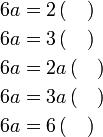
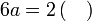
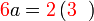
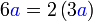
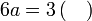
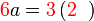
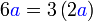
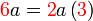
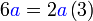
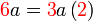
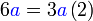
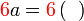
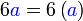
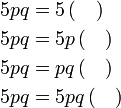
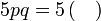
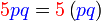
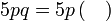
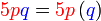
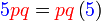
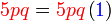
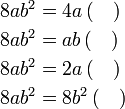
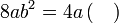
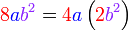
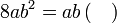
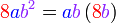
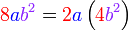
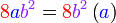
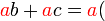
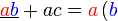


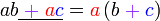
%2bc)).png)
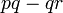
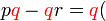
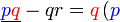
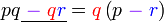
-r)).png)